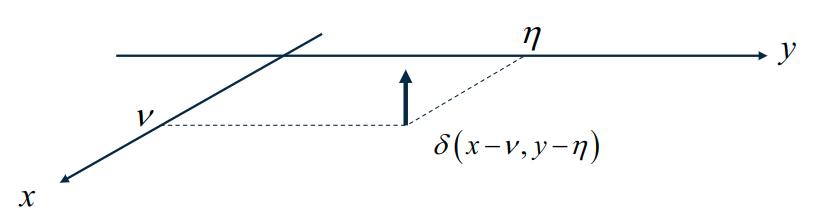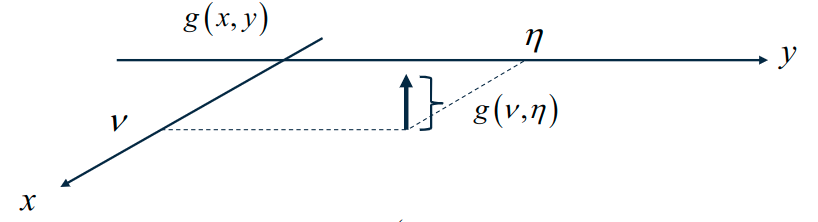Informatik/Bildverarbeitung in der Medizin 1.md

Einführung - Übersicht Bildverarbeitungsprozess

Bildverarbeitung

Bildverarbeitung / Bildanalyse

• Wissenschaft von der algorithmischen Verarbeitung von Informationen in Bildern
• Ziel: Ableitung relevanter (nützlicher) Parameter
• Anwendung in nahezu allen Bereichen von Wissenschaft und Technik, Medizin und Alltag

Vorlesung BVM

• Grundlagen der Digitalen Bildverarbeitung
• Anwendungsfokus: Medizinische Bildverarbeitung

Anwendungsfelder digitaler Bildverarbeitung

• Medizinische Diagnostik und Therapie
  • Röntgen, CT, DSA, PET, SPECT, Ultraschall, MRI, fMRI, OCT
• Biolog. Bildgebung
  • Histologie, Mikroskopie, Zählung, Klassifikation u. Morphologie von Zellen, Bewegungsanalyse, Wachstum
• Forensik / Rechtsmedizin
  • Fingerabdruck, Gesichtserkennung
• Mensch-Maschine-Kommunikation / Robotik
  • Gestenerkennung, Zeichensprache, Orientierung im Raum
• Dokumentenverarbeitung
  • Automatische Texterkennung (OCR), Scannen, Archivieren, Fotografie
• Industrie / Materialforschung
  • Qualitätssicherung, automatisches Zählen, Komponentenerkennung
• Remote Sensing
  • Ernte, Wetter, Vermessung, Militär, Astronomie

Medizinische Bildverarbeitung

• Anwendungsfelder
  • Diagnose
  • Screening
  • OP-Planung
  • Bestrahlungsplanung
  • Ausbildung
• Eigenschaften
  • Große Komplexität / multimodal (verschiedene bildgebende Verfahren)
  • Variabilität der Objekte /individuelle Unterschiede
  • Große Bedeutung feinster Strukturen
  • Dreidimensionale / dynamische Bilddaten
  • Vergleichbarkeit mit Standardfällen
  • Hohe Robustheit notwendig

Modellgestützte Interpretation

• Bildinformationen
  • Modell- bzw. anwendungsspezifische Interpretation des Bildes
  • Bild nur unter Erwartungshaltung bzw. mit Hilfe eines Modells interpretierbar
  • Können verfälscht oder widersprüchlich sein
• Bildrestauration
  • ''Pin Cushion'' Verzerrung, ''Barrel'' Verzerrung
  • Verzerrung durch Bewegung (Restauration durch inverse Filterung)
  • Fokussierungsunschärfe
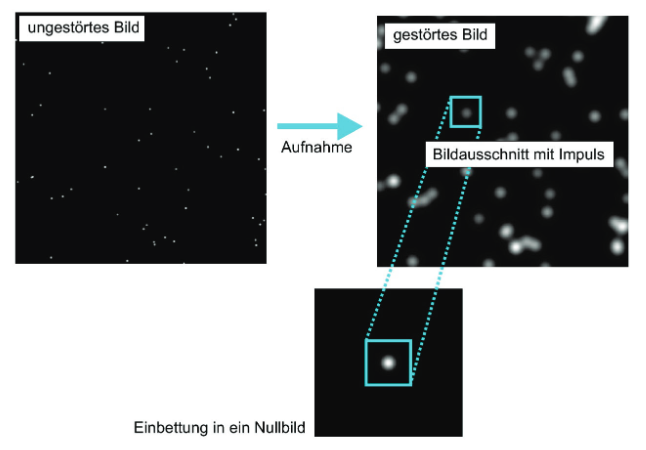
  • Verrauschtes Bild -> Gauß-Filter
  • ,,Salz und Pfeffer'' Rauschen -> Medianfilter
  • Kontraständerung
• Bildregistrierung
• Segmentierung
  • Schwellwertsegmentierung
  • Erkennung von Kreisen (Hough-Transformation)
• Merkmale und Klassifikation

Vorlesungsinhalt

0. Einführung
   • Bildverarbeitungsprozess
1. Bildrepräsentation und Bildeigenschaften
   • Ortsbereich
   • Spektralbereich
   • Diskrete 2D-Faltung
2. Bildvorverarbeitung
   • Bildrestauration
   • Bildregistrierung
   • Bildverbesserung
3. Segmentierung
   • Pixel- bzw. histogrammbasierteSegmentierung
   • Regionen-basierte Segmentierung
   • Kantenbasierte Segmentierung
   • Wasserscheidentransformation
   • Modellbasierte Segmentierung
4. Morphologische Operationen
   • Morphologische Basisoperationen
   • Entfernen von Segmentierungsfehlern
   • Bestimmung von Formmerkmalen
5. Merkmalsextraktion und Klassifikation
   • RegionenbasierteMerkmale
   • Formbasierte Merkmale
   • Einführung in die Klassifikation

Bildrepräsentation und Bildeigenschaften im Ortsbereich

Ortsbereich

Kontinuierliche Bilder

Wiederholung: Kontinuierliche Signale

Das kontinuierliche Signal

Definition: x(t)\in\mathbb{R} eindimensionale Funktion

• kontinuierliche Zeitvariable t\in\mathbb{R}
• Funktionswert x = kontinuierlicher Signalwert (Spannung, Strom, ...)

Dirac Stoß

• Definition: \inf_{-\infty}^{\infty} \delta(t) dt=1, \delta(t)=\begin{cases}\rightarrow\infty\quad \text{ für } t=0\\ 0\quad\text{ für } t\not= 0\end{cases}
• Approximation (Definition): \delta(t)=lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon}* rect(\frac{t}{\epsilon})
• Symmetrie \delta(-t)=\delta(t)
• Stoßgewicht \inf_{-\infty}^{\infty} a\delta(t)dt = a
• Ausblendeigenschaft (Siebeigenschaft) u(t)*\delta(t-\tau)=u(\tau)*\delta(t-\tau)
• Faltung \inf_{-\infty}^{\infty} u(t)*\delta(t-\tau)d\tau = u(t)*\delta(t)=u(t)
• Verschiebung u(t)*\delta(t-\tau)=u(t-\tau)
• Fourier Transformierte \delta(t) \laplace 1, 1\Laplace \delta(f)

1D Faltung

• Definition: u_1(t)*u_2(t)=\inf_{-\infty}{\infty} u_1(\tau) * u_2(t-\tau) d\tau
• Kommutativgesetz: u_1(t)*u_2(t)=u_2(t)*u_1(t)
• Assoziativgesetz: [u_1(t)*u_2(t)]*u_3(t)=u_1(t)*[u_2(t)*u_3(t)]
• Distributivgesetz: u_1(t)*[u_2(t)+u_3(t)]= u_1(t)*u_2(t) + u_1(t)*u_3(t)
• Neutrales Element: (Einheitselement) u(t)*\delta(t)=\inf_{-\infty}^{\infty} u(\tau)*\delta(t-\tau)d\tau = u(t)
• 

LTI (Linear Time-Invariant) Systeme

• x(t)\rightarrow LTI System g(t) \rightarrow y(t)
• Eingang/Ausgang: y(t)=x(t)*g(t) \fourier Y(f)=X(f)*G(f)
• Kausalität g(t)=0 gilt falls t<0
• BIBO Stabilität \inf_{-\infty}^{\infty} |g(t)|dt < \infty
• Sprungantwort / Stoßantwort
  • h(t)=\inf_{-\infty}^t g(\tau)d\tau
  • g(t)=\frac{d}{dt} h(t)

Kontinuierliche Bilder

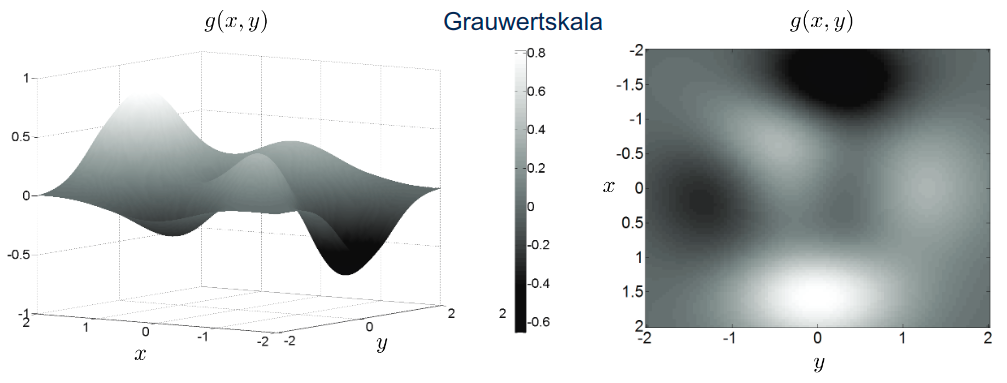
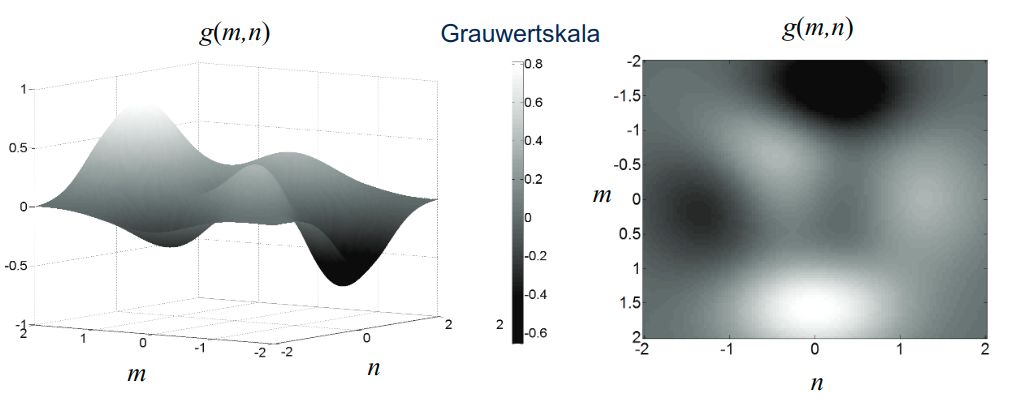
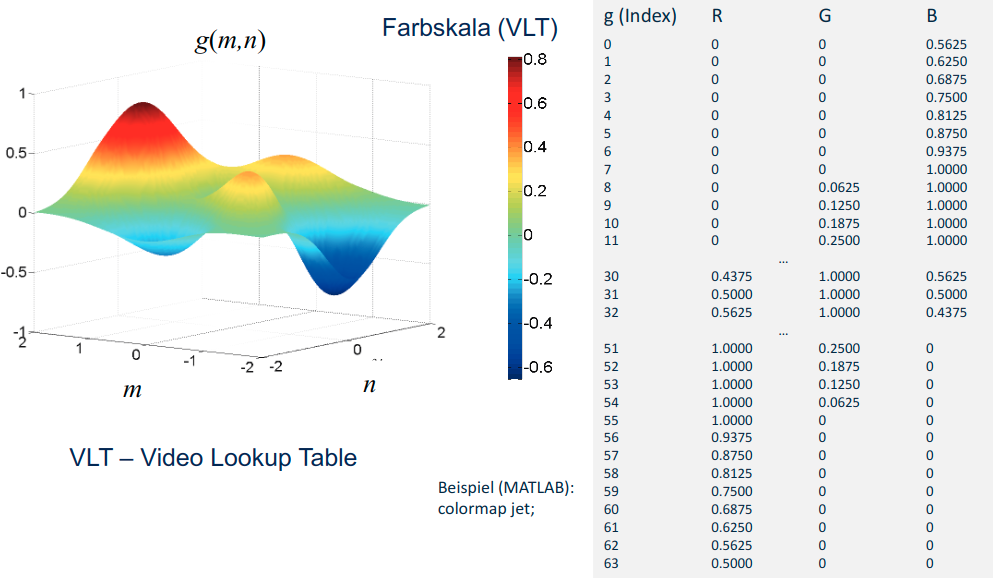
Das kontinuierliche Bild: Definition als 2D-Grauwertfunktion

Definition: g(x, y) \in\mathbb{R} \rightarrow zweidimensionale Funktion

• g: Funktionswert = kontinuierlicher Grauwert (Lichtstärke oder Schwächung von Röntgenstrahlung)
• kontinuierliche Ortsvariablen x und y: x,y\in\mathbb{R}

Alternativ: g(\underline{r})\in\mathbb{R} mit \underline{r}=\binom{x}{y}\in\mathbb{R}^2 mit Ortsvektor \underline{r}

Bild als 2D Grauwertfunktion:

Beispiel 2D Rechteck

• g(x,y)=rect(x,y)=\begin{cases} 1\quad\text{ für } |x,y|\leq 0,5\\ 0 \quad\text{ sonst}\end{cases}
• g(x,y)=rect(x,y)=rect(x)*rect(y)=g_1(x)*g_2(y)
• ...ist eine separierbare Funktion, d.h. g(x,y)=g_1(x)*g_2(y)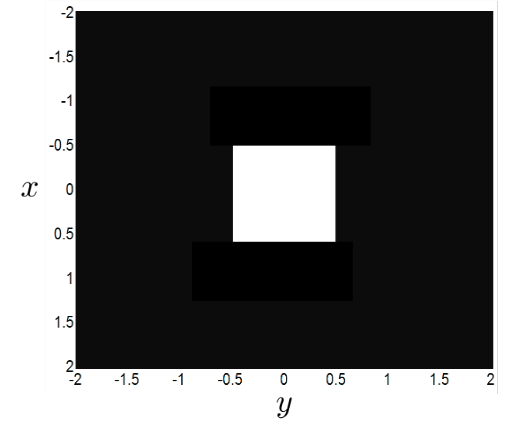
• 

Beispiel: 2D Rechteck skaliert

• g(x,y)=rect(\frac{x}{\epsilon_x}, \frac{y}{\epsilon_y})=\begin{cases} 1\quad\text{ für } |\frac{x}{\epsilon_x},\frac{y}{\epsilon_y}\leq 0,5 \\ 0\quad\text{ sonst } \end{cases}
• g(x,y)=rect(\frac{x}{\epsilon_x}= rect(\frac{x}{\epsilon_x}) * rect(\frac{y}{\epsilon_y})
• ... ist eine separierbare Funktion, d.h.: g(x,y)=g_1(x)*g_2(y)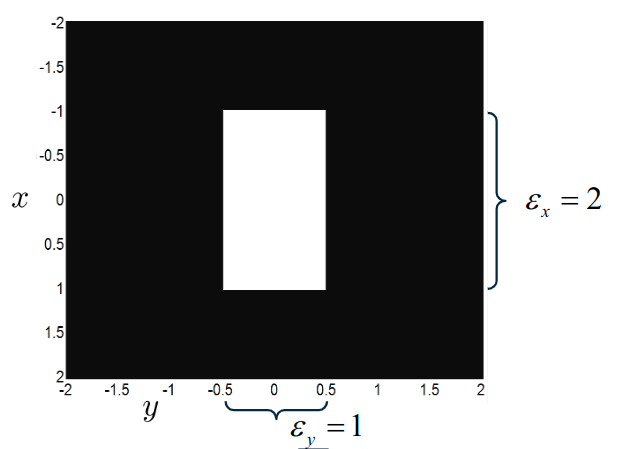
• 

Beispiel: Approximation des 2D Dirac-Stoßes

• \delta(x,y)=lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon^1} * rect(\frac{x}{\epsilon},\frac{y}{\epsilon})
• ... ist ebenso separierbar, d.h.: \delta(x,y)=\delta(x)*\delta(y)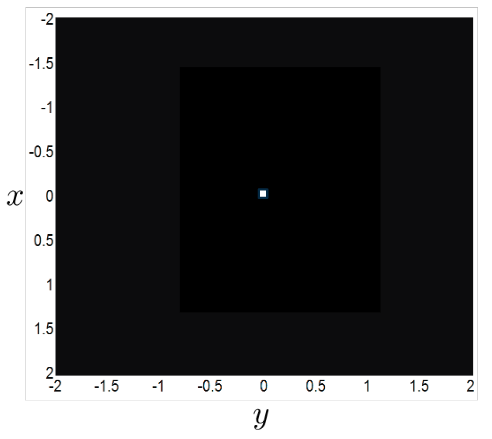
• 

2D-Dirac-Stoß

• Definition: \delta(x,y)=\begin{cases} \rightarrow\infty \quad\text{ für } x,y=0 \\ 0 \quad\text{ für } x,y\not=0\end{cases}
• \inf_{-\infty}^{\infty} \inf_{-\infty}^{\infty} \delta(x,y)dx dy=1
• Verschobener Dirac-Stoß: \delta(x-v, y-\eta)
  • 
• Abtasteigenschaft (Ausblendeigenschaft)
  • 
  • weil \inf_{-\infty}^{\infty} \inf_{-\infty}^{\infty} \delta(x,y)dx dy=1
  • g(v,\eta)=\inf_{-\infty}^{\infty} \inf_{-\infty}^{\infty} g(x,y) * \delta(x-v, y-\eta) dx dy
  • Mit Hilfe eines um v, \eta verschobenen 2D-Dirac-Stoßes lässt sich g(x,y) an den Ortskoordinaten v,\eta abtasten \rightarrow g(v,\eta)
• 2D-Faltung mit Dirac Stoß: g(x,y)=\inf_{-\infty}^{\infty} \inf_{-\infty}^{\infty} g(x,y) * \delta(x-v, y-\eta) dv d\eta = g(x,y) ** \delta(x,y)
  • Die Faltung eines Bildes g(x,y) mit dem 2D-Dirac-Stoß ergibt wieder das Bild g(x,y).
  • \delta(x,y)= Einheitselement (neutrales Element) der 2D Faltung

Lineare kontinuierliche Operatoren / Point Spread Function

Eigenschaft: g_2(x,y)=U\{g_1(x,y)\}

Linearität: O\{a_1g_{11} (x,y) +a_2g_{22}(x,y)\}=a_1*O\{g_{11}(x,y)\} + a_2*O\{g_{22}(x,y)\}

Ein- / Ausgangsbeziehung: g_2(x,y) = Ο\{g_1(x,y)\}= \inf_{-\infty}^{\infty}\inf_{-\infty}^{\infty} g_1(v,\eta)*O\{\delta(x-v,y-\eta)\} dv dn

Impulsantwort (Point Spread Function) g_2(x,y)=\inf_{-\infty}^{\infty}\inf_{-\infty}^{\infty} g_1(v,\eta)*h(x,y,v,\eta)dv d\eta

Für räumlich invariante (verschiebungsinvariante) Operatoren gilt: h(x,y,v,\eta)=O\{\delta(x-v,y-\eta)\}=h(x-v,y-\eta)

2D-Faltung mit der Impulsantwort des linearen Operators (Point SpreadFunction): g_2(x,y)=\inf_{-\infty}^{\infty}\inf_{-\infty}^{\infty} g_1(v,\eta)*h(x-v,y-\eta)dv dn = g_1(x,y) * * h(x,y)

Point Spread Function (PSF)

Beispiel Fokussierungsunschärfe

Beispiel Bewegung

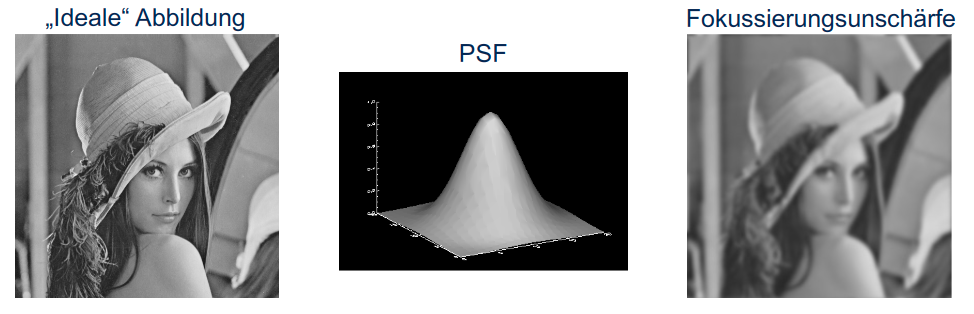
Digitale Bilder

Diskretisierung und Quantisierung

Digitalisierung: Diskretisierung der Ortsvariablen

Abtastfunktion: s(x,y)=\sum_{m=-\infty}^{\infty} \sum_{n=-\infty}^{\infty} \delta(x-m*\Delta x, y-n*\Delta y)

Abtastung: g_A(x,y)=s(x,y)*g(x,y)=\sum_{n=-\infty}^{\infty} \sum_{m=-\infty}^{\infty} g(m*\Delta x, n*\Delta y)* \delta(x-m*\Delta x, y-n*\Delta y)= A_{\Delta x, \Delta y}\{g(x,y)\}

Repräsentation des ortsdiskreten Bildes unabhängig von \Delta x, \Delta y: \rightarrow g_A(m,n) (,,2D-Zahlenfolge'')

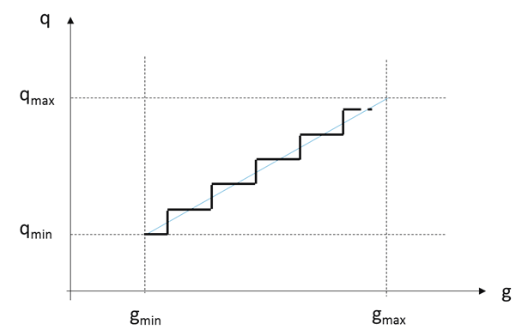
Digitalisierung: Quantisierung der Grauwerte

q(g)=[\frac{g-g_{min}}{g_{max}-g_{min}} * (q_{max}-q_{min}) +q_{min}]_{mathbb{N}} (Runden auf nächste natürliche Zahl)

häufig wird q_{min}=0 gewählt: q(g)=[\frac{g-g_{min}}{g_{max}-g_{min}}*q_{max}]_{mathbb{N}}

q_{max}=2^N -1, N Auflösung des AD-Wandlers

Digitale Bildrepräsentation

Pixel

Grauwertbild

Falschfarbendarstellung

Nachbarschaft, Pfad, Zusammenhang und Distanzmaße

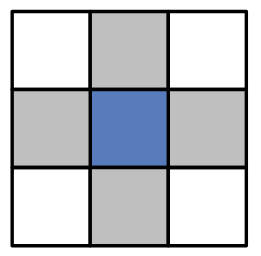
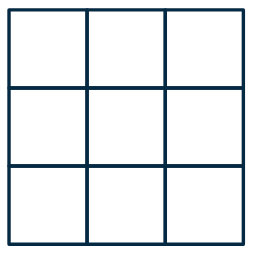
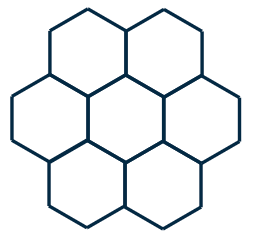
Nachbarschaften

• 4er-Nachbarschaft
  • Nachbarpixel: gemeinsame Kante
  • 
• 8er-Nachbarschaft
  • Nachbarpixel: gemeinsame Kante oder Ecke
  • 
• Regelmäßige 2D-Gitter
  • Dreieckgitter
    • 
    • 3-Nachbarschaft
    • 12-Nachbarschaft
  • Quadratisches Gitter
    • 
    • 4-Nachbarschaft
    • 8-Nachbarschaft
  • Hexagonales Gitter
    • 
    • 6-Nachbarschaft

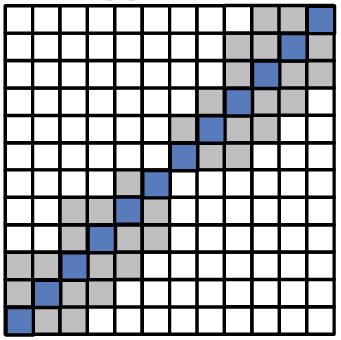
Pfad:

• Zwei Pixel P_A(m_A,n_A) und P_B(m_B,n_B) sind durch einen Pfad verbunden, falls es eine Folge von benachbarten Pixeln (P_A, P_1, ..., P_B) gibt, für die eine Homogenitätsbedingung (z.B. alle Pixel haben gleichen Grauwert, d.h. g(P_A)=g(P_1)=...=g(P_B)) gilt.
• Offener Pfad: P_A \not= P_B
• Geschlossener Pfad: P_A = P_B
• Pfade sind an Nachbarschaftsdefinitionen gebunden!

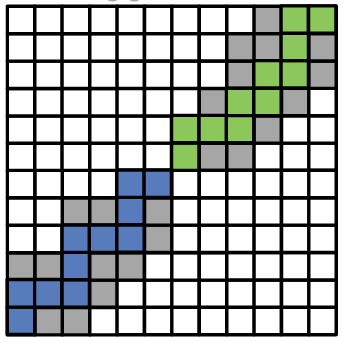
Zusammenhang: Eine Menge von Pixeln ist zusammenhängend, wenn zwischen zwei beliebigen Pixeln ein Pfad existiert.

Zusammenhang: Definition gemäß Nachbarschaftsbeziehung

• Zusammenhang gemäß 4-Nachbarschaft
  • Die beiden grauen Regionen sind unter 4-Nachbarschaft nicht zusammenhängend (kein verbindender Pfad vorhanden).
  • Der Hintergrund ist unter Annahme der komplementären8-Nachbarschaft zusammenhängend.
  • 
• Zusammenhang gemäß 8-Nachbarschaft
  • Die beiden grauen Regionen sind unter 8-Nachbarschaft zusammenhängend (verbindender Pfad vorhanden).
  • Der Hintergrund ist unter Annahme der komplementären4-Nachbarschaft nicht zusammenhängend.
  • 
• Die Nachbarschaftsdefinitionen in Vorder-und Hintergrund sollten komplementär sein!

Rand:

• Der Rand einer zusammenhängenden Pixelmenge M ist eine Folge von Pixeln in M, die mindestens einen Nachbarn haben, der nicht zu M gehört.
• Die Randpixel gehören somit zu M dazu.
• Der Rand ist ein zusammenhängender Pfad und deshalb auch an eine Nachbarschaftsdefinition gebunden.

Rand: Definition gemäß Nachbarschaftsbeziehung

• Rand in 4 - Nachbarschaft zum Hintergrund
  • Jedes Randpixel hat mind. einen Nachbarn in 4-Nachbarschaft, der nicht zu M gehört.
  • Rand = zusammenhängender Pfad gemäß 8-Nachbarschaft
  • 
• Rand in 8 - Nachbarschaft zum Hintergrund
  • Jedes Randpixel hat mind. einen Nachbarn in 8-Nachbarschaft, der nicht zu M gehört.
  • Rand = zusammenhängender Pfad gemäß 4-Nachbarschaft
  • 

Distanzmaße zwischen zwei Pixeln

Euklidische Distanz

• Länge der direkten Verbindung
• D_E= ||P_1-P_2||_2=\sqrt{(m_1-,_2)^2 + (n_1-n_2)^2}
• Euklidische Norm N=2, p=2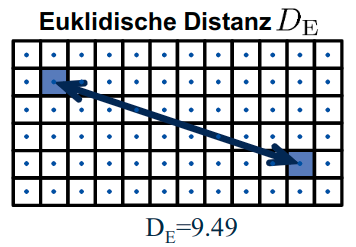
• 

Manhattan-Distanz (City-Block)

• Länge des kürzesten Pfades unter 4er-Nachbarschaft
• D_4=||P_1-P_2||_1=|m_1 - m_2|+|n_1-n_2|
• Summennorm N=2, p=1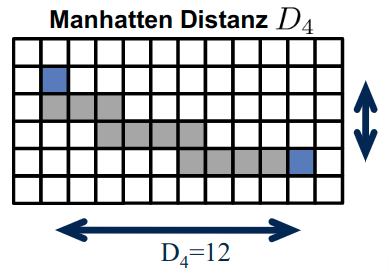
• 

Schachbrett-Distanz

• Länge des kürzesten Pfades unter 8er-Nachbarschaft
• D_8 = ||P_1-P_2||_{\infty} = max\{|m_1-m_2|, |n_1 -n_2|\}
• Maximalnorm N=2, p=\infty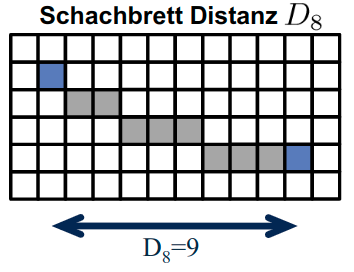
• 

Normangabe der Distanzmaße

• p-Norm: ||x||_p = (\sum_{i=1}^N |x_i|^p )^{\frac{1}{p}} mit x_1=m_1-m_2 und x_2=n_1-n_2
• Euklidische Norm: N=2, p=2, D_E=(\sum_{i=1}^2 |x_i|^2)^{frac{1}{2}}=\sqrt{x_1^2 + x_2^2}
• Summennorm: N=2, p=1, D_4=(\sum_{i=1}^2 |x_i|)= x_1+x_2
• Maximalnorm: N=2, p=\infty, D_8=lim_{p\rightarrow\infty}(x^p_{max} + (ax_{max})^p)^{\frac{1}{p}} = lim_{p\rightarrow\infty} (x_{max}^p (1+a^p))^{\frac{1}{p}} = x_{max} mit a<1 weil lim_{p\rightarrow\infty}(a^p)=0
• D_8\leq D_E \leq D_4
  • 
  • 
  • 
• Schachbrett Distanz \leq Euklidische Distanz \leq Manhatten Distanz

Literaturempfehlungen

• Wilhelm Burger and MarkJ. Burge, ,,Digitale Bildverarbeitung – eine algorithmische Einführung mit Java'', Springer, 3. Auflage, 2015
• Klaus D. Tönnies, ,,Grundlagen der Bildverarbeitung'', Pearson Studium, 1. Auflage, 2005
• Heinz Handels, ,,Medizinische Bildverarbeitung'', Vieweg+Teubner, 2. Auflage, 2009
• Bernd Jähne, ,,Digitale Bildverarbeitung'', Springer, 6. Auflage, 2005
• Angelika Erhardt, ,,Einführung in die Digitale Bildverarbeitung'', Vieweg+Teubner, 1.Auflage, 2008
• Rafael C. Gonzales and Richard E. Woods, ,,Digital Image Processing'', Pearson International, 3. Edition,2008
• Geoff Dougherty, ,,Digital Image Processing for Medical Applications'', Cambridge University Press, 1. Edition, 2009
• William K. Pratt, ,,DigitalImageProcessing'', Wiley, 4. Edition, 2007
• John L. Semmlow, ,,Biosignal and Medical Image Processing'', CRCPress, 2. Edition, 2009