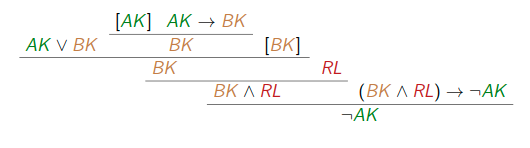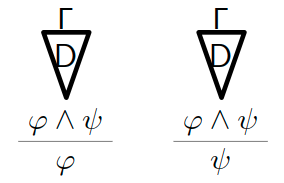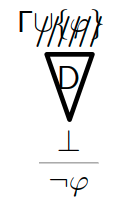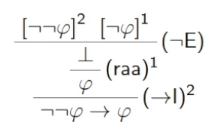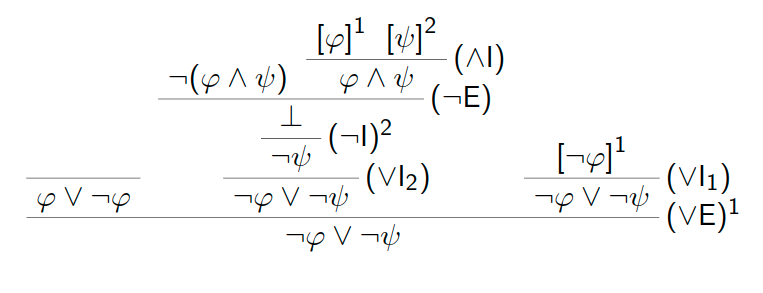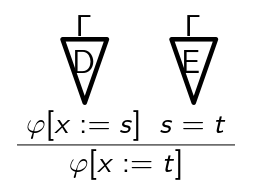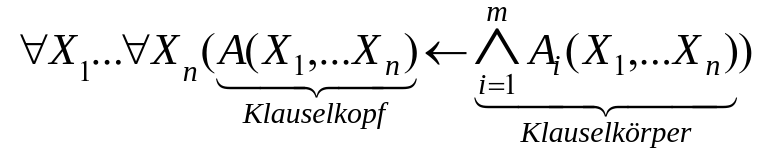Informatik/Logik und Logikprogrammierung.md

Logik

Die Logik

• versucht, gültige Argumentationen von ungültigen zu unterscheiden,
• hat Anwendungen in der Informatik,
• formalisiert die zu untersuchenden Aussagen und
• beschränkt sich auf einen wohldefinierten Teil der möglichen Aussagen => es gibt verschiedene "Logiken", z.B. "Aussagen-" und "Prädikatenlogik"
  • daneben:
    • temporale Logiken (Mastervorlesung "Verifikation")
    • modale Logiken
    • epistemische Logiken
    • ...

Syllogismen

Aristoteles (384-322 v.Chr.) untersuchte das Wesen der Argumentation und des logischen Schließens mit dem Ziel, korrekte von inkorrekten Argumenten zu unterscheiden. Verschiedene Werke, u.a. Analytica priora, Analytica posteriora.

Aristoteles nennt die logischen Schlußfolgerungen Syllogismen (griechisch: "Zusammenrechnung").

Ein Syllogismus ist eine Aussage, in der bestimmte Dinge [die Prämissen] behauptet werden und in der etwas anderes [die Konsequenz], unumgänglich aus dem Behaupteten folgt. Mit dem letzten Satz meine ich, dass die Prämissen die Konsequenz zum Resultat haben, und damit meine ich, dass keine weitere Prämisse erforderlich ist, um die Konsequenz unumgänglich zu machen.

Beispiele

Wenn alle Menschen sterblich sind und
Sokrates ein Mensch ist,
dann ist Sokrates sterblich.

Wenn eine Zahl gerade und größer als zwei ist,
dann ist sie keine Primzahl.

Wenn die Leitzinsen hoch sind,
dann sind die Börsianer unzufrieden.

Aristoteles identifizierte einige zulässige Syllogismen, die Scholastiker fügten weitere hinzu:

(Barbara)

Alle Dackel sind Hunde                  Alle P sind M
Alle Hunde sind Tiere                   Alle M sind S
Dann sind alle Dackel Tiere             Alle P sind S

(Cesare)

Keine Blume ist ein Tier                Kein P ist M
Alle Hunde sind Tiere                   Alle S sind M
Dann ist keine Blume ein Hund           Kein P ist S

(Darapti)

Alle Delfine leben im Meer              Alle M sind P
Alle Delfine sind Säugetiere            Alle M sind S
Dann leben einige Säugetiere im Meer    Einige S sind P

Kalküle

Gottfried Wilhelm Leibniz (1646-1716) wollte korrekte von inkorrekten Argumentationsketten unterscheiden. Hierzu sollte ein Kalkül entwickelt werden, in dem alle korrekten Argumentationsketten ermöglicht sind (und keine inkorrekten).

David Hilbert (1862-1943) entwickelte solche Kalküle. Diese "Hilbertkalküle" sind sehr verschieden von üblichen Argumentationsmustern.

Gerhard Gentzen (1909-1945) entwickelte Kalküle des "natürlichen Schließens", die übliche Argumentationsmuster formalisieren.

Die Aussagenlogik

George Boole (1815 - 1864) entwickelte einen Kalkül zum Rechnen mit atomare Aussagen, die entweder wahr oder falsch sein können.

Verknüpfung durch Operatoren(und, oder, nicht, wenn-dann... ).

Die Prädikatenlogik (Ende des 19. Jahrhunderts)

Gottlob Frege (1848-1925), Giuseppe Peano (1858-1932) und Bertrand Russell (1872-1970)entwickelten die Logik zur Grundlage der Mathematik, als formale Basis für die Vermeidung von Widersprüchen. Entwicklung der Prädikatenlogik, die erlaubt:

• Beziehungen zwischen "Objekten" zu beschreiben
• existentielle Aussagen zu treffen: "es gibt ein x, so dass... "
• universelle Aussage zu treffen: "für jedes x gilt, dass... "

Logik in der Informatik

Claude Shannon (1916 - 2001) benutzt die Aussagenlogik 1937, um elektromechanische Schaltkreise zu beschreiben und zu optimieren.

Allen Newell (1927-1992), Herbert Simon (1916-2001) und Alan Robinson (1930-2016) entwickelten 1950-1960 die ersten Systeme für die Automatisierung des logischen Schließens als Werkzeug der Künstlichen Intelligenz.

• Schaltkreisentwurf: Schaltkreise lassen sich durch logische Formeln darstellen -> Entwurf und Optimierung von Schaltungen
• Modellierung und Spezifikation: Eindeutige Beschreibung von komplexen Systemen
• Verifikation: Beweisen, dass ein Programm das gewünschte Verhalten zeigt
• Datenbanken: Formulierung von Anfragen an Datenbanken -> Abfragesprache SQL (Structured Query Language)
• (klassische) Künstliche Intelligenz:
  • Planung
  • Mensch-Maschine Kommunikation
  • Theorembeweiser: Der Computer beweist mathematische Sätze -> automatischer Beweis von wichtigen Sätzen im Bereich der Booleschen Algebren
• Logische Programmiersprachen

Außerdem: Logik ist ein Paradebeispiel für Syntax und formale Semantik

Edsger W. Dijkstra (1920-2002): Informatik = VLSAL (Very large scale application of logics)

Die Logik

• versucht, gültige Argumentationen von ungültigen zu unterscheiden,
• hat Anwendungen in der Informatik,
• formalisiert die zu untersuchenden Aussagen

Probleme mit natürlicher Sprache

1. Problem: Zuordnung von Wahrheitswerten zu natürlichsprachigen Aussagen ist problematisch.
   • Beispiele:
     • Ich habe nur ein bißchen getrunken.
     • Sie hat sich in Rauch aufgelöst.
     • Das gibt es doch nicht!
     • Rache ist süß.
2. Problem: Natürliche Sprache ist oft schwer verständlich.
   • Beispiel: Auszug aus der "Analytica Priora" von Aristoteles
   • Die Aussage: Wenn der Mittelbegriff sich universell auf Ober- oder Untersatz bezieht, muss ein bestimmter negativer Syllogismus resultieren, immer wenn der Mittelbegriff sich universell auf den Obersatz bezieht, sei es positiv oder negativ, und besonders wenn er sich auf den Untersatz bezieht und umgekehrt zur universellen Aussage.
   • Der Beweis: Denn wenn M zu keinem N gehört, aber zu einem O, ist es notwendig, dass N zu einem O nicht gehört. Denn da die negative Aussage umsetzbar ist, wird N zu keinem M gehören: Aber es war erlaubt, dass M zu einem O gehört: Deshalb wird N zu einem O nicht gehören: Denn das Ergebnis wird durch die erste Figur erreicht. Noch einmal: Wenn M zu allen N gehört, aber nicht zu einem O, ist es notwendig, dass N nichtzu einem O gehört: Denn wenn N zu allen O gehört und M auch alle N-Eigenschaften zugeschrieben werden, muss M zu allen O gehören: Aber wir haben angenommen, dass M zu einem O nicht gehört. Und wenn M zu allen N gehört, aber nicht zu allen O, können wir folgern, dass N nicht zu allen O gehört: Der Beweis ist der gleiche wie der obige. Aber wenn M alle O-Eigenschaften zugeschrieben werden, aber nicht alle N-Eigenschaften, wird es keinen Syllogismus geben.
3. Problem:Natürliche Sprache ist mehrdeutig.
   • Beispiel: "Ich sah den Mann auf dem Berg mit dem Fernrohr."
     • (((Ich sah den Mann) auf dem Berg) mit dem Fernrohr)
     • ((Ich sah (den Mann auf dem Berg)) mit dem Fernrohr)
     • ((Ich sah den Mann) (auf dem Berg mit dem Fernrohr))
     • (Ich sah ((den Mann auf dem Berg) mit dem Fernrohr))
     • (Ich sah (den Mann (auf dem Berg mit dem Fernrohr)))
4. Problem:Natürliche Sprache hängt von Kontext ab.

Die Beatles sind Musiker
Paul McCartney ist ein Beatle
Paul McCartney ist ein Musiker

Die Beatles sind vier
Paul McCartney ist ein Beatle
Paul McCartney ist vier

Kapitel 1: Aussagenlogik

Beispiel

Ein Gerät besteht aus einem Bauteil A, einem Bauteil B und einem roten Licht. Folgendes ist bekannt:

1. Bauteil A oder Bauteil B (oder beide) sind kaputt.
2. Wenn Bauteil A kaputt ist, dann ist auch Bauteil B kaputt.
3. Wenn Bauteil B kaputt ist und das rote Licht leuchtet, dann ist Bauteil A nicht kaputt.
4. Das rote Licht leuchtet.

Zur Formalisierung verwenden wir folgende Abkürzungen:

• RL (rotes Licht leuchtet),
• AK (Bauteil A kaputt),
• BK (Bauteil B kaputt),
• \vee (oder),
• \rightarrow (wenn, dann),
• \wedge (und) und
• \lnot (nicht).

Damit können wir unser Wissen kompakter hinschreiben:

1. AK \vee BK
2. AK \rightarrow BK
3. (BK \wedge RL)\rightarrow \lnot AK
4. RL

Aus den vier Aussagen lassen sich weitere Aussagen neue Aussagen bilden 5. Falls AK gilt, so folgt aus AK\rightarrow BK, dass BK gilt. 6. Falls BK gilt, so gilt natürlich BK. 7. Da AK \vee BK gilt, folgt aus (5) und (6), dass BK in jedem Fall gilt. 8. Es gilt auch RL. 9. Also gilt BK\wedge RL (aus (7) und (8)). 10. Es gilt auch (BK \wedge RL)\rightarrow\lnot AK. 11. Also gilt \lnot AK (aus (9) und (10)).

Damit sind wir überzeugt, dass das Bauteil A heil ist.

Den Beweis, dass das Teil A heil ist, werden wir als "Beweisbaum" formalisieren:

In der Aussagenlogik gehen wir von "Aussagen" aus, denen wir (zumindest prinzipiell) Wahrheitswerte zuordnen können.

Beispiele

• Die Summe von 3 und 4 ist 7.
• Jana reagierte aggressiv auf Martins Behauptungen.
• Jede gerade natürliche Zahl>2 ist Summe zweier Primzahlen.
• Alle Marsmenschen mögen Pizza mit Pepperoni.
• Albert Camus était un écrivain français.
• In theory, practically everything is possible.

Für diese Aussagen verwenden wir dieatomaren Formeln p,q,r bzw. p_0,p_1,...

Die Aussagen werden durch "Operatoren" verbunden. Beispiele

• ... und...
• ... oder...
• nicht...
• wenn... dann...
• entweder... oder... , aber nicht beide.
• mehr als die Hälfte der Aussagen ... gilt.

Für solche zusammengesetzten Aussagen verwenden wir \varphi,\psi usw.

Durch die Wahl der erlaubten Operatoren erhält man unterschiedliche "Logiken".

Da der Wahrheitswert einer zusammengesetzten Aussage nur vom Wahrheitswert der Teilaussagen abhängen soll, sind Operatoren wie "weil" oder "obwohl" nicht zulässig.

Syntax der Aussagenlogik

Eine atomare Formel hat die Form p_i (wobei i\in\mathbb{N}=\{0,1,...\}). Formeln werden durch folgenden induktiven Prozess definiert:

1. Alle atomaren Formeln und \bot sind Formeln.
2. Falls \varphi und \psi Formeln sind, sind auch $(\varphi\wedge\psi),(\varphi\wedge\psi)$(\varphi \rightarrow\psi)und $\lnot\varphi$Formeln.
3. Nichts ist Formel, was sich nicht mittels der obigen Regeln erzeugen läßt.

Beispielformel: \lnot((\lnot p_4 \vee p_1)\wedge\bot)

Bezeichnungen:

• Falsum: \bot
• Konjunktion: \wedge
• Disjunktion: \vee
• Implikation: \rightarrow
• Negation: \lnot

Abkürzungen p,q,r... statt p_0,p_1,p_2...

(\bigvee_{i=1}^n \varphi_i statt (...((\varphi_1\vee\varphi_2)\vee\varphi_3)\vee...\vee\varphi_n)

(\bigwedge_{i=1}^n \varphi_i) statt (...((\varphi_1\wedge\varphi_2)\wedge\varphi_3)\wedge...\wedge\varphi_n)

(\varphi \leftrightarrow \psi) statt ((\varphi\rightarrow\psi)\wedge(\psi\rightarrow\varphi))

Präzedenz der Operatoren:

• \leftrightarrow bindet am schwächsten
• \rightarrow...
• \vee...
• \wedge...
• \lnot bindet am stärksten

Es gilt also z.B.: (\alpha\leftrightarrow\beta\vee\lnot\gamma\rightarrow\sigma\wedge\lnot\eta) = (\alpha\leftrightarrow ((\beta\vee\lnot\gamma)\rightarrow(\sigma\wedge\lnot\eta)))

Dennoch: Zu viele Klammern schaden i.A. nicht.

Natürliches Schließen

Ein (mathematischer) Beweis zeigt, wie die Behauptung aus den Voraussetzungen folgt.
Analog zeigt ein "Beweisbaum" (= "Herleitung" = "Deduktion"), wie eine Formel der Aussagenlogik aus Voraussetzungen (ebenfalls Formeln der Aussagenlogik) folgt.
Diese "Deduktionen" sind Bäume, deren Knoten mit Formeln beschriftet sind:

• an der Wurzel steht die Behauptung (= Konklusion \varphi)
• an den Blättern stehen Voraussetzungen (= Hypothesen oder Annahmen aus \Gamma)
• an den inneren Knoten stehen "Teilergebnisse" und "Begründungen"

Konstruktion von Deduktionen

Aus der Annahme der Aussage \varphi folgt \varphi unmittelbar: eine triviale Deduktion

\varphi mit Hypothesen \{\varphi\} und Konklusion \varphi.

Folgend werden wir

• überlegen, wie aus "einfachen mathematischen Beweisen" umfangreichere entstehen können und
• parallel dazudefinieren, wie aus einfachen Deduktionen umfangreichere konstruiert werden können.

Konjunktion

Konjunktionseinführung in math. Beweisen

Ein mathematischer Beweis einer Aussage "\varphi und $\psi$" sieht üblicherweise so aus:

• "Zunächst zeige ich \varphi: ... (hier steckt die eigentliche Arbeit)
• Jetzt zeige ich \psi: ... (nochmehr eigentliche Arbeit)
• Also haben wir "\varphi und $\psi$" gezeigt. qed"

Konjunktionseinführung (ausführlich)

Ist D eine Deduktion von \varphi mit Hypothesen aus \Gamma und ist E eine Deduktion von \psi mit Hypothesen aus \Gamma, so ergibt sich die folgende Deduktion von \varphi\wedge\psi mit Hypothesen aus \Gamma:

Kurzform: \frac{\varphi\quad\psi}{\varphi\wedge\psi} (\wedge I)

Konjunktionselimination (ausführlich)

Ist D eine Deduktion von \varphi\wedge\psi mit Hypothesen aus \Gamma, so ergeben sich die folgenden Deduktionen von \varphi bzw. von \psi mit Hypothesen aus \Gamma:

Kurzform: \frac{\varphi\wedge\psi}{\varphi} (\wedge E_1) \quad\quad \frac{\varphi\wedge\psi}{\psi} (\wedge E_2)

Beispiel

Wir zeigen \varphi\wedge\psi unter der Hypothese \psi\wedge\varphi:...

Dies ist eine Deduktion mit Konklusion \varphi\wedge\psi und Hypothese \psi\wedge\varphi (zweimal verwendet).

Implikation

Implikationseinführung in math. Beweisen

Ein mathematischer Beweis einer Aussage "Aus \varphi folgt $\psi$" sieht üblicherweise so aus:

• "Angenommen, \varphi gilt.
• Dann ... (hier steckt die eigentliche Arbeit).
• Damit gilt \psi.
• Also haben wir gezeigt, dass \psi aus \varphi folgt. qed"

Die Aussage \varphi ist also eine "temporäre Hypothese".

Implikationseinführung (ausführlich)

Ist D eine Deduktion von \psi mit Hypothesen aus \Gamma\cup\{\varphi\}, so ergibt sich die folgende Deduktion von \varphi\rightarrow\psi mit Hypothesen aus \Gamma:

Kurzform $[\varphi]$ $\vdots$ \frac{\psi}{\varphi\rightarrow\psi} (\rightarrow I)

Beispiel: ... Dies ist eine Deduktion von \varphi\rightarrow\varphi ohne Hypothesen.

Implikationselimination in math. Beweisen

Ein mathematischer Beweis einer Aussage "\psi gilt" über eine Hilfsaussage sieht so aus:

• "Zunächst zeigen wir, dass \varphi gilt: ...
• Dann beweisen wir, dass \psi aus \varphi folgt: ...
• Also haben wir \psi gezeigt. qed"

Implikationselimination oder modus ponens (ausführlich)

Ist D eine Deduktion von \varphi mit Hypothesen aus \Gamma und ist E eine Deduktion von \varphi\rightarrow\psi mit Hypothesen aus \Gamma, so ergibt sich die folgende Deduktion von \psi mit Hypothesen aus \Gamma:

Kurzform: \frac{\varphi\quad \varphi\rightarrow\psi}{\psi} (\rightarrow E)

Beispiel

Bemerkung: die Indizes 1, 2 und 3 machen deutlich, welche Hypothese bei welcher Regelanwendung gestrichen wurde. Deduktionen können recht groß werden.

Diese Deduktion hat keine Hypothesen!

Disjunktion

Disjunktionselimination oder Fallunterscheidung in math. Beweisen

Ein mathematischer Beweis einer Aussage "\sigma gilt" mittels Fallunterscheidung sieht üblicherweise so aus:

• "Zunächst zeigen wir, dass \varphi\vee\psi gilt: ...
• Gilt \varphi, so gilt \sigma, denn ...
• Gilt \psi, so gilt ebenfalls \sigma, denn ...
• Also haben wir gezeigt, dass \sigma gilt. qed"

Die Aussagen \varphi und \psi sind also wieder "temporäre Hypothesen".

Disjunktionselimination oder Fallunterscheidung (ausführlich)

Ist D eine Deduktion von \varphi\vee\psi mit Hypothesen aus \Gamma, ist E eine Deduktion von \sigma mit Hypothesen aus $\Gamma\cup{\varphi}$und ist F eine Deduktion von \sigma mit Hypothesen aus \Gamma\cup\{\psi\}, so ergibt sich die folgende Deduktion von \sigma mit Hypothesen aus \Gamma:

Disjunktionselimination Kurzform: $\quad [\psi] \quad[\varphi]$ $\quad \vdots \quad\vdots$ \frac{\varphi\vee\psi \quad\sigma \quad\sigma}{\sigma} (\vee E)

Disjunktionseinführung (Kurzform) \frac{\varphi}{\varphi\vee\psi} (\vee I_1) \quad \frac{\psi}{\varphi\vee\psi} (\vee I_2)

Negation

Negationseinführung in math. Beweisen

Ein mathematischer Beweis einer Aussage "\varphi gilt nicht" sieht so aus:

• "Angenommen,$\varphi$gilt.
• Dann folgt 0=1, denn .... Mit anderen Worten, dies führt zu einem Widerspruch.
• Also haben wir gezeigt, dass \varphi nicht gilt. qed"

Die Aussage \varphi ist also wieder eine "temporäre Hypothese".

Negationseinführung (ausführlich)

Ist D eine Deduktion von \bot mit Hypothesen aus \Gamma\cup\{\varphi\}, so ergibt sich die folgende Deduktion von \lnot\varphi mit Hypothesen aus \Gamma:

Kurzform: $[\varphi]$ $\vdots$ \frac{\bot}{\lnot\varphi} (\lnot I)

Negationselimination (ausführlich)

Ist D eine Deduktion von \lnot\varphi mit Hypothesen aus \Gamma und ist E eine Deduktion von \varphi mit Hypothesen aus \gamma, so ergibt sich die folgende Deduktion von \bot mit Hypothesen aus \Gamma:

Kurzform: \frac{\lnot\varphi \quad \varphi}{\bot} (\lnot E)

Falsum

Hat man "$0=1$" bewiesen, so ist man bereit, alles zu glauben: ex falso sequitur quodlibet

ausführlich: Ist D eine Deduktion von \bot mit Hypothesen aus \Gamma, so ergibt sich die folgende Deduktion von \varphi mit Hypothesen aus \Gamma:

Kurzform: \frac{\bot}{\varphi} (\bot)

math. Widerspruchsbeweis

Ein indirekter Beweis einer Aussage "\varphi gilt" sieht üblicherweise so aus:

• "Angenommen, \varphi gilt nicht, d.h. \lnot\varphi gilt.
• Dann folgt 0=1, d.h. ein Widerspruch.
• Also haben wir gezeigt, dass \varphi gilt. qed"

Die Aussage \lnot\varphi ist also wieder eine "temporäre Hypothese".

reductio ad absurdum (ausführlich)

Ist D eine Deduktion von \bot mit Hypothesen aus \Gamma\cup\{\lnot\varphi\}, so ergibt sich die folgende Deduktion von \varphi mit Hypothesen aus \Gamma:

Kurzform: $[\lnot\varphi]$ $\vdots$ \frac{\bot}{\varphi} (raa)

Regeln des natürlichen Schließens

Definition

Für eine Formelmenge \Gamma und eine Formel \varphi schreiben wir \Gamma\Vdash\varphi wenn es eine Deduktion gibt mit Hypothesen aus \Gamma und Konklusion \varphi. Wir sagen "\varphi ist eine syntaktische Folgerung von $\Gamma$".

Eine Formel \varphi ist ein Theorem, wenn \varnothing\Vdash\varphi gilt.

Bemerkung

\Gamma\Vdash\varphi sagt (zunächst) nichts über den Inhalt der Formeln in \Gamma\cup\{\varphi\} aus, sondern nur über die Tatsache, dass \varphi mithilfe des natürlichen Schließens aus den Formeln aus \Gamma hergeleitet werden kann.

Ebenso sagt "\varphi ist Theorem" nur, dass \varphi abgeleitet werden kann, über "Wahrheit" sagt dieser Begriff (zunächst) nichts aus.

Satz

Für alle Formeln \varphi und \psi gilt \{\lnot(\varphi\vee\psi)\}\Vdash\lnot\varphi\wedge\lnot\psi.

Beweis: Wir geben eine Deduktion an...

• ${\lnot\varphi\wedge\lnot\psi}\Vdash\lnot(\varphi\vee\psi)$
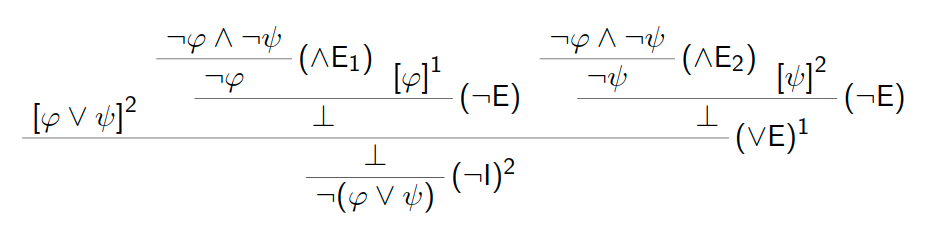
• ${\lnot\varphi\vee\lnot\psi}\Vdash\lnot(\varphi\wedge\psi)$
• ${\varphi\vee\psi} \Vdash \psi\vee\varphi$

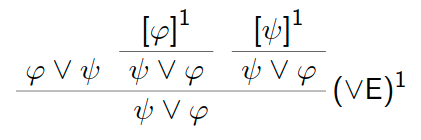
Satz

Für jede Formel \varphi ist \lnot\lnot\varphi\rightarrow\varphi ein Theorem.

Beweis: Wir geben eine Deduktion mit Konklusion \lnot\lnot\varphi\rightarrow\varphi ohne Hypothesen an...

Satz

Für jede Formel \varphi ist \varphi\vee\lnot\varphi ein Theorem.

Beweis: Wir geben eine Deduktion mit Konklusion \varphi\vee\lnot\varphi ohne Hypothesen an...

Bemerkung: Man kann beweisen, dass jede Deduktion der letzten beiden Theoreme die Regel (raa) verwendet, sie also nicht "intuitionistisch" gelten.

Satz

\{\lnot(\varphi\wedge\psi)\}\Vdash\lnot\varphi\vee\lnot\psi

Semantik

Formeln sollen Verknüpfungen von Aussagen widerspiegeln, wir haben dies zur Motivation der einzelnen Regeln des natürlichen Schließens genutzt. Aber die Begriffe „syntaktische Folgerung“ und „Theorem“ sind rein syntaktisch definiert.

Erst die jetzt zu definierende „Semantik“ gibt den Formeln „Bedeutung“.

Idee der Semantik: wenn man jeder atomaren Formel p_i einen Wahrheitswertzuordnet, so kann man den Wahrheitswert jeder Formel berechnen.

Es gibt verschiedene Möglichkeiten, Wahrheitswerte zu definieren:

• zweiwertige oder Boolesche Logik B=\{0,1\}: Wahrheitswerte „wahr“=1 und „falsch“= 0
• dreiwertige Kleene-Logik K_3=\{0,\frac{1}{2},1\}: zusätzlicher Wahrheitswert „unbekannt“=\frac{1}{2}
• Fuzzy-Logik F=[0,1]: Wahrheitswerte sind „Grad der Überzeugtheit“
• unendliche Boolesche Algebra $B_R$= Menge der Teilmengen von \mathbb{R}; A\subseteq\mathbb{R} ist „Menge der Menschen, die Aussage für wahr halten“
• Heyting-Algebra $H_R$= Menge der offenen Teilmengen von \mathbb{R}
  • Erinnerung: A\subseteq\mathbb{R} offen, wenn \forall a\in A\exists\epsilon >0:(a-\epsilon,a+\epsilon)\subseteq A, d.h., wenn A abzählbare Vereinigung von offenen Intervallen (x,y) ist.

Beispiele:

• offen: (0,1), \mathbb{R}_{>0}, \mathbb{R}\backslash\{0\}, \mathbb{R}\backslash\mathbb{N}
• nicht offen: [1,2), \mathbb{R}_{\geq 0}, \mathbb{Q}, \mathbb{N}, \{\frac{1}{n} | n\in\mathbb{N}\}, \mathbb{R}\backslash\mathbb{Q}

Sei W eine Menge von Wahrheitswerten.\ Eine W-Belegung ist eine Abbildung B:V\rightarrow W, wobei V\subseteq\{p_0 ,p_1 ,...\} eine Menge atomarer Formeln ist.

Die W-Belegung B:V\rightarrow W paßt zur Formel \phi, falls alle atomaren Formeln aus \phi zu V gehören.

Sei nun B eine W-Belegung. Was ist der Wahrheitswert der Formel p_0\vee p_1 unter der Belegung B?

Zur Beantwortung dieser Frage benötigen wir eine Funktion \vee_W :W\times W\rightarrow W (analog für \wedge,\rightarrow,\lnot).

Wahrheitswertebereiche

Definition: Sei W eine Menge und R\subseteq W\times W eine binäre Relation.

• R ist reflexiv, wenn (a,a)\in R für alle a\in W gilt.
• R ist antisymmetrisch, wenn (a,b),(b,a)\in R impliziert, dass a=b gilt (für alle a,b\in W).
• R ist transitive, wenn (a,b),(b,c)\in R impliziert, dass (a,c)\in R gilt (für alle a,b,c\in W).
• R ist eine Ordnungsrelation, wenn R reflexiv, antisymmetrisch und transitiv ist. In diesem Fall heißt das Paar (W,R) eine partiell geordnete Menge.

Beispiel

1. Sei \leq übliche Ordnung auf $\mathbb{R}$und W\subseteq\mathbb{R}. Dann ist (W,\leq) partiell geordnete Menge.
2. Sei X eine Menge und W\subseteq P(X). Dann ist (W,\subseteq) partiell geordnete Menge.
3. Sei W=P(\sum ∗) und \leq_p die Relation „es gibt Polynomialzeitreduktion“ (vgl. „Automaten, Sprachen und Komplexität“). Diese Relation ist reflexiv, transitiv, aber nicht antisymmetrisch (denn 3-SAT\leq_p HC und HC\leq_p_3-SAT).

Definition: Sei (W,\leq) partiell geordnete Menge, M\subseteq W und a\in W.

• a ist obere Schranke von M, wenn m\leq a für alle m\in M gilt.
• a ist kleinste obere Schranke oder Supremum von M, wenn a obere Schranke von M ist und wenn a\leq b für alle oberen Schranken b von M gilt. Wir schreiben in diesem Fall a=sup \ M.
• a ist untere Schranke von M, wenn a\leq m für alle m\in M gilt.
• a ist größte untere Schranke oder Infimum von M, wenn a untere Schranke von M ist und wenn b\leq a für alle unteren Schranken b von M gilt. Wir schreiben in diesem Fall a=inf\ M.

Beispiel

1. betrachte (W,\leq) mit W=\mathbb{R} und \leq übliche Ordnung auf \mathbb{R}.
   • Dann gelten sup[0,1] = sup(0,1) =1.
   • sup\ W existiert nicht (denn W hat keine obere Schranke).
2. betrachte (W,\subseteq) mit X Menge und W =P(X).
   • sup\ M=\bigcup_{A\in M} A für alle M\subseteq W
3. betrachte (W,\subseteq) mit W=\{\{0\},\{1\},\{0,1,2\},\{0,1,3\}\}.
   • sup\{\{0\},\{0,1,2\}\}=\{0,1,2\}
   • \{0,1,2\} und \{0,1,3\} sind die oberen Schranken von M=\{\{0\},\{1\}\}, aber M hat kein Supremum

Definition: Ein (vollständiger) Verband ist eine partiell geordnete Menge (W,\leq), in der jede Menge M\subseteq W ein Supremum sup\ M und ein Infimum inf\ M hat. In einem Verband (W,\leq) definieren wir:

• 0_W = inf\ W und 1_W= sup\ W
• a\wedge_W b= inf\{a,b\} und a\vee_W b= sup\{a,b\} für a,b\in W

Bemerkung: In jedem Verband (W,\leq) gelten 0_W= sup\ \varnothing und 1_W= inf\ \varnothing (denn jedes Element von W ist obere und untere Schranke von \varnothing).

Definition: Ein Wahrheitswertebereich ist ein Tupel (W,\leq,\rightarrow W,\lnot W), wobei (W,\leq) ein Verband und \rightarrow W:W^2 \rightarrow W und \lnot W:W\rightarrow W Funktionen sind.

Beispiel

• Der Boolesche Wahrheitswertebereich B ist definiert durch die Grundmenge B=\{0,1\}, die natürliche Ordnung \leq und die Funktionen \lnot_B (a) = 1-a, \rightarrow_B(a,b) = max(b, 1 -a). Hier gelten:
  • 0_B=0, 1_B= 1,
  • a\wedge_B b= min(a,b), a\vee_B b= max(a,b)
• Der Kleenesche Wahrheitswertebereich K_3 ist definiert durch die Grundmenge K_3=\{0,\frac{1}{2},1\} mit der natürlichen Ordnung \leq und durch die Funktionen \lnot_{K_3} (a) = 1 -a , \rightarrow_{K_3} (a,b) = max(b, 1-a). Hier gelten:
  • \lnot_{K_3} = 0, 1_{K_3} = 1
  • a\wedge_{K_3} b= min(a,b), a\vee_{K_3} b= max(a,b)
• Der Wahrheitswertebereich F der Fuzzy-Logik ist definiert durch die Grundmenge F=[0,1]\subseteq\mathbb{R} mit der natürlichen Ordnung \leq und durch die Funktionen \lnot_F (a) = 1-a, \rightarrow_F (a,b) = max(b, 1-a). Hier gelten:
  • 0_F= 0, 1_F= 1
  • a\wedge_F b= min(a,b), a\vee_F b= max(a,b)
• Der Boolesche Wahrheitswertebereich B_R ist definiert durch die Grundmenge B_R=\{A|A\subseteq \mathbb{R}\} mit der Ordnung \subseteq und durch die Funktionen \lnot_{B_R} (A) =\mathbb{R}\backslash A, \rightarrow_{B_R} (A,B) = B\cup\mathbb{R}\backslash A. Hier gelten:
  • 0_{B_R}=\varnothing, 1_{B_R}=\mathbb{R}
  • A\wedge_{B_R} B=A\cap B, A\vee_{B_R} B=A\cup B
• Der Heytingsche Wahrheitswertebereich H_R ist definiert durch die Grundmenge H_{mathbb{R}} =\{A\subseteq\mathbb{R} | \text{A ist offen}\}, die Ordnung \subseteq und durch die Funktionen \lnot_{H_R} (A) = Inneres(\mathbb{R}\backslash A), \rightarrow_{H_R} (A,B) =Inneres(B\cup \mathbb{R}\backslash A). Hier gelten:
  • 0_{H_R}=\varnothing, 1_{H_R}=\mathbb{R}
  • A\wedge_{H_R} B= A\cap B, A\vee_{H_R} B=A\cup B
  • Erinnerung: Inneres(A) =\{a\in A|\exists \epsilon > 0 : (a-\epsilon,a+\epsilon)\subseteq A\}
  • Beispiele: Inneres((0,1))=(0,1)=Inneres([0,1]),Inneres(N)=\varnothing,Inneres(\mathbb{R}_{\geq 0}) = \mathbb{R}_{> 0}

Sei W ein Wahrheitswertebereich und B eine W-Belegung. Induktiv über den Formelaufbau definieren wir den Wahrheitswert \hat{B}(\phi)\in W jeder zu B passenden Formel \phi:

• \hat{B}(\bot) = 0_W
• \hat{B}(p) = B(p) falls p eine atomare Formel ist
• \hat{B}((\phi\wedge \psi )) = \hat{B}(\phi)\wedge_W \hat{B}(\psi )
• \hat{B}((\phi\vee \psi )) = \hat{B}(\phi)\vee_W \hat{B}(\psi )
• \hat{B}((\phi\rightarrow \psi )) = \rightarrow W(\hat{B}(\phi),\hat{B}(\psi ))
• \hat{B}(\lnot\phi) = \lnot W(\hat{B}(\phi))

Wir schreiben im folgenden B(\phi) anstatt \hat{B}(\phi).

Beispiel: Betrachte die Formel \phi= ((p\wedge q)\rightarrow (q\wedge p)).

• Für eine beliebige B-Belegung B:\{p,q\}\rightarrow B gilt B((p\wedge q)\rightarrow (q\wedge p)) = max(B(q\wedge p), 1 -B(p\wedge q)) = max(min(B(q),B(p)), 1 -min(B(p),B(q))) = 1 = 1_B
• Für die $K_3$-Belegung B:\{p,q\}\rightarrow K_3 mit $B(p) =B(q) = \frac{1}{2}$} gilt B((p\wedge q)\rightarrow (q\wedge p)) = max(B(q\wedge p), 1 -B(p\wedge q))= max(min(B(q),B(p)), 1 -min(B(p),B(q))) = \frac{1}{2} \not= 1_{K_3}
• analog gibt es eine F-Belegung B:\{p,q\}\rightarrow F, so dass B((p\wedge q)\rightarrow (q\wedge p)) \not = 1_F gilt.
• Für eine beliebige $H_{mathbb{R}}$-Belegung B:\{p,q\}\rightarrow H_R gilt B((p\wedge q)\rightarrow (q\wedge p)) = Inneres(B(q\wedge p)\cup \mathbb{R}\backslash B(p\wedge q)) = Inneres((B(q)\cap B(p))\cup \mathbb{R}\backslash (B(p)\cap B(q))) = Inneres(\mathbb{R}) = \mathbb{R} = 1_{H_R}

Folgerung und Tautologie

Sei W ein Wahrheitswertebereich. Eine Formel \phi heißt eine W-Folgerung der Formelmenge \Gamma, falls für jede W-Belegung B, die zu allen Formeln aus \Gamma \cup\{\phi\} paßt, gilt: inf\{B(\gamma )|\gamma \in \Gamma \}\leq B(\phi)

Wir schreiben \Gamma \Vdash W\phi, falls \phi eine W-Folgerung von \Gamma ist.

Bemerkung: Im Gegensatz zur Beziehung \Gamma \vdash \phi, d.h. zur syntaktischen Folgerung, ist \Gamma \Vdash W \phi eine semantische Beziehung.

Eine W-Tautologie ist eine Formel \phi mit \varnothing \Vdash W\phi, d.h. B(\phi) = 1_W für alle passenden W-Belegungen B (denn inf\{\hat{B}(\gamma )|\gamma \in \varnothing \}= inf \varnothing = 1_W).

Wahrheitstafel für den Booleschen Wahrheitswertebereich B:

RL	AK	BK	AK\vee BK	AK\rightarrow BK	(BK\wedge RL)\rightarrow\lnot AK	RL	\lnot AK
0	0	0	0	1	1	0	1
0	0	1	1	1	1	0	1
0	1	0	1	0	1	0	0
0	1	1	1	1	1	0	0
1	0	0	0	1	1	1	1
1	0	1	1	1	1	1	1
1	1	0	1	0	1	1	0
1	1	1	1	1	0	1	0

Wir erhalten also ${(AK\vee BK),(AK\rightarrow BK), ((BK\wedge RL)\rightarrow \lnot AK),RL} \Vdash_B \lnot AK$ und können damit sagen:

„Wenn die Aussagen „Bauteil A oder Bauteil B ist kaputt“ und „daraus, dass Bauteil A kaputt ist, folgt, dass Bauteil B kaputt ist“ und... wahr sind, ... dann kann man die Folgerung ziehen: die Aussage „das Bauteil A ist heil“ ist wahr.“

Erinnerung aus der ersten Vorlesung: \{(AK\vee BK),(AK\rightarrow BK), ((BK\wedge RL)\rightarrow \lnot AK),RL\} \vdash \lnot AK

Beispiel Sei \phi beliebige Formel mit atomaren Formeln in V.

• Sei B:V\rightarrow B eine B-Belegung. Dann gilt

  B(\lnot\lnot\phi\rightarrow\phi) = \rightarrow B(\lnot B\lnot B(B(\phi)),B(\phi)) = max(B(\phi), 1 -( 1 -( 1 -B(\phi)))) = max(B(\phi), 1 -B(\phi)) = 1 = 1_B.

  Also ist \lnot\lnot\phi\rightarrow\phi eine B-Tautologie (gilt ebenso für den Wahrheitswertebereich B_R).

• Sei B:V\rightarrow H_R eine $H_R$-Belegung mit B(\phi) =R\backslash\{0\}. Dann gelten

  • B(\lnot\phi) = Inneres(\mathbb{R}\backslash B(\phi)) = Inneres(\{0\}) =\varnothing
  • B(\lnot\lnot\phi) = Inneres(\mathbb{R}\backslash B(\lnot\phi)) = Inneres(\mathbb{R}) = \mathbb{R}
  • B(\lnot\lnot\phi\rightarrow\phi) = \rightarrow_{H_R} (B(\lnot\lnot\phi),B(\phi)) = \rightarrow_{H_R} (\mathbb{R},\mathbb{R}\backslash \{0\}) = Inneres(\mathbb{R}\backslash\{0\}\cup\mathbb{R}\backslash\mathbb{R}) = \mathbb{R}\backslash\{0\}\not =\mathbb{R}= 1_{H_R}

  Also ist \lnot\lnot\phi\rightarrow\phi keine $H_R$-Tautologie (gilt ebenso für die Wahrheitswertebereiche K_3 und F).

• Sei B:V\rightarrow B eine B-Belegung. Dann gilt

  B(\phi\vee\lnot\phi) = max(B(\phi), 1 -B(\phi)) = 1 = 1_B.

  Also ist \phi\vee\lnot\phi eine B-Tautologie (gilt ebenso für den Wahrheitswertebereich B_R).

• Sei B:V\rightarrow H_R eine $H_R$-Belegung mit B(\phi)=\mathbb{R}\backslash\{0\}. Dann gilt B(\phi\vee\lnot\phi) = B(\phi)\cup B(\lnot\phi) = \mathbb{R}\backslash\{0\}\cup \varnothing \not= 1_{H_R}.

  Also ist \phi\vee\lnot\phi keine $H_R$-Tautologie (gilt ebenso für die Wahrheitswertebereiche K_3 und F).

• Sei B:V\rightarrow B eine B-Belegung. Dann gilt

  B(\lnot\phi\rightarrow\bot) = \rightarrow_B(B(\lnot\phi),B(\bot)) = max(0,1-B(\lnot \phi)) = 1 -( 1 -B(\phi)) =B(\phi)$.

  Also haben wir \{\lnot\phi\rightarrow\bot\}\Vdash B\phi und \{\phi\}\Vdash B\lnot \phi\rightarrow\bot.

  • Ebenso erhält man:
    • \{\lnot\phi\rightarrow\bot\}\Vdash_{K_3} \phi
    • \{\phi\}\Vdash_{K_3} \lnot\phi\rightarrow\bot
    • \{\lnot\phi\rightarrow\bot\}\Vdash_F\phi
    • \{\phi\}\Vdash F\lnot\phi\rightarrow\bot

• Sei B:D\rightarrow H_R eine $H_R$-Belegung mit B(\phi) =\mathbb{R}\backslash\{0\}. Dann gilt B(\lnot\phi\rightarrow\bot) = Inneres(B(\bot )\cup \mathbb{R}\backslash B(\lnot\phi))= Inneres(\varnothing \cup \mathbb{R}\backslash\varnothing)= \mathbb{R} \not\supseteq B(\phi).

  also \{\lnot\phi\rightarrow\bot\}\not\Vdash_{H_R} \phi.

  Es gilt aber \{\phi\}\Vdash_{H_R}\lnot \phi\rightarrow\bot.

Zusammenfassung der Beispiele

	B	B_R	K_3	F	H_R
\varnothing\Vdash_W\lnot\lnot\phi\rightarrow\phi	√	√	–	–	–	\varnothing\vdash \lnot\lnot\phi\rightarrow\phi
\varnothing\Vdash_W\phi\vee\lnot\phi	√	√	–	–	–	\varnothing\vdash\phi\vee\lnot\phi
\{\lnot\phi\rightarrow\bot\}\Vdash_W\phi	√	√	√	√	–	\{\lnot\phi\rightarrow\bot\}\vdash\phi
\{\phi\}\Vdash_W\lnot\phi\rightarrow\bot	√	√	√	√	√	\{\phi\}\vdash\lnot\phi\rightarrow\bot

• √ in Spalte W:W-Folgerung gilt
• - in Spalte W:W-Folgerung gilt nicht

Überblick: Wir haben definiert

• \Gamma\vdash\phi syntaktische Folgerung
  • Theorem („hypothesenlos ableitbar“)
• \Gamma\Vdash_W \phi (semantische) W-Folgerung
  • W-Tautologie („wird immer zu 1_W ausgewertet“)

Frage: Was ist die Beziehung zwischen diesen Begriffen, insbes. zwischen „Theorem“ und „W-Tautologie“? Da z.B. B-Folgerung $\not =K_3$-Folgerung, hängt die Anwort von W ab.

Korrektheit

Können wir durch mathematische Beweise zu falschen Aussagenkommen?

Können wir durch das natürliche Schließen zu falschen Aussagen kommen?

Existiert eine Menge \Gamma von Formeln und eine Formel \varphi mit \Gamma\vdash\varphi und \Gamma\not\Vdash_W \varphi? Für welche Wahrheitswertebereiche W?

Frage für diese Vorlesung: Für welche Wahrheitswertebereiche W gilt $\Gamma\vdash\varphi\Rightarrow\Gamma\vdash_W \varphi$ bzw. \varphi ist Theorem \Rightarrow\varphi ist W-Tautologie?

Beispiel: Betrachte den Kleeneschen Wahrheitswertebereich K_3.

• Sei p atomare Formel. $\frac{[p]^4}{p\rightarrow p}$ Also gilt \varnothing\vdash p\rightarrow p, d.h. p\rightarrow p ist Theorem.
• Sei B $K_3$-Belegung mit B(p)=\frac{1}{2}. Dann gilt B(p\rightarrow p) = max(B(p), 1-B(p)) =\frac{1}{2}, also inf\{B(\gamma)|\gamma\in\varnothing\}= 1 >\frac{1}{2} = B(p\rightarrow p). Damit haben wir gezeigt \varnothing\not\Vdash_{K_3} p\rightarrow p.

Die Implikation \Gamma\vdash\varphi\Rightarrow\Gamma\vdash_W \varphi gilt also NICHT für den Kleeneschen Wahrheitswertebereich W=K_3 und damit auch NICHT für den Wahrheitswertebereich der Fuzzy-Logik F.

Korrektheitslemma für nat. Schließen & Wahrheitswertebereich B

Sei D eine Deduktion mit Hypothesen in der Menge \Gamma und Konklusion \varphi. Dann gilt \Gamma\vdash_B \varphi, d.h. inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\varphi) für alle passenden B-Belegungen B.

Beweis: Induktion über die Größe der Deduktion D (d.h. Anzahl der Regelanwendungen).

• I.A.: die kleinste Deduktion D hat die Form \varphi mit Hypothese \varphi und Konklusion \varphi. Sei B passendeB-Belegung. Hypothesen von D in \Gamma\Rightarrow\varphi\in\Gamma\Rightarrow inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\varphi)\Rightarrow\Gamma\vdash_B \varphi
• I.V.: Behauptung gelte für alle Deduktionen, die kleiner sind als D.
• I.S.: Wir unterscheiden verschiedene Fälle, je nachdem, welche Regel als letzte angewandt wurde.
  • (\wedge I) Die Deduktion hat die Form $\frac{\alpha\quad\beta}{\alpha\wedge\beta}$ mit \varphi=\alpha\wedge\beta. Sei B passende B-Belegung. Nach IV gelten inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\alpha) und $inf{B(\gamma)|\gamma\in\Gamma}\leq B(\beta)$ und damit inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\alpha)\wedge_B B(\beta)=B(\alpha\wedge\beta) =B(\varphi). Da B beliebig war, haben wir \Gamma\vdash_B \varphi gezeigt.
  • (\vee E) Die Deduktion D hat die Form $\frac{\alpha\vee\beta\quad\phi\quad\phi}{\phi}$ Also gibt es Deduktion E mit Hypothesen in \Gamma und Konklusion \alpha\vee\beta und Deduktionen F und G mit Hypothesen in \Gamma\cup\{\alpha\} bzw. \Gamma\cup\{\beta\} und Konklusion \varphi. Sei B passende B-Belegung. Nach IV gelten inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\alpha\vee\beta) (1) inf\{B(\gamma)|\gamma\in\Gamma\cup\{\alpha\}\}\leq B(\varphi) (2) inf\{B(\gamma)|\gamma\in\Gamma\cup\{\beta\}\}\leq B(\varphi) (3) Wir unterscheiden zwei Fälle:
    • B(\alpha)\leq B(\beta): inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\alpha\vee\beta) =B(\alpha)\vee_B B(\beta) =B(\beta) impliziert inf\{B(\gamma)|\gamma\in\Gamma\}= inf\{B(\gamma)|\gamma\in\Gamma\cup\{\beta\}\}\leq B(\varphi)
    • B(\alpha)>B(\beta): analog Da B beliebig war, haben wir \Gamma\vdash_B \varphi gezeigt.
  • (\rightarrow I) Die DeduktionDhat die Form $\frac{\beta}{\alpha\rightarrow\beta}$ mit \varphi=\alpha\rightarrow\beta. Sei B eine passende B-Belegung. Nach IV gilt $inf{B(\gamma)|\gamma\in\Gamma\cup{\alpha}}\leq B(\beta)$ Wir unterscheiden wieder zwei Fälle:
    • B(\alpha)=0:inf\{B(\gamma)|\gamma\in\Gamma\}\leq 1 =\rightarrow_B(B(\alpha),B(\beta)) = B(\alpha\rightarrow\beta) =B(\varphi)
    • $B(\alpha)=1:inf{B(\gamma)|\gamma\in\Gamma}=inf{B(\gamma)|\gamma\in\Gamma\cup{\alpha}}\leq B(\beta) =\rightarrow_B (B(\alpha),B(\beta)) = B(\alpha\rightarrow\beta) =B(\varphi)$ Da B beliebig war, habe wir \Gamma\vdash_B \varphi gezeigt.
  • (raa) Die DeduktionDhat die Form $\frac{\bot}{\phi}$ Sei B eine passende B-Belegung. Nach IV gilt inf\{B(\gamma)|\gamma\in\Gamma\cup\{\lnot\varphi\}\}\leq B(\bot) = 0. Wir unterscheiden wieder zwei Fälle:
    • inf\{B(\gamma)|\gamma\in\Gamma\}=0: dann gilt inf\{B(\gamma)|\gamma\in\Gamma\}\leq B(\varphi).
    • inf\{B(\gamma)|\gamma\in\Gamma\}=1: Wegen inf\{B(\gamma)|\gamma\in\Gamma\cup\{\lnot\varphi\}\}=0 folgt 0 =B(\lnot\varphi)=\lnot_B (B(\varphi)) und daher B(\varphi)=1\geq inf\{B(\gamma)|\gamma\in\Gamma\}. Da B beliebig war, haben wir \Gamma\vdash_B \varphi gezeigt.

Ist die letzte Schlußregel in der Deduktion D von der Form (\wedge I), (\vee E), (\rightarrow I) oder (raa), so haben wir die Behauptung des Lemmas gezeigt. Analog kann dies für die verbleibenden Regeln getan werden.

Korrektheitssatz für natürliches Schließen & Wahrheitswertebereich B

Für jede Menge von Formeln \Gamma und jede Formel \varphi gilt \Gamma\vdash\varphi\Rightarrow\Gamma\vdash_B\varphi.

Beweis: Wegen \Gamma\vdash\varphi existiert eine Deduktion D mit Hypothesen in \Gamma und Konklusion \varphi. Nach dem Korrektheitslemma folgt \Gamma\vdash_B \varphi.

Korollar: Jedes Theorem ist eine B-Tautologie.

Korrektheitssatz für natürliches Schließen & Wahrheitswertebereich B

Für jede Menge von Formeln \Gamma und jede Formel \varphi gilt \Gamma\vdash\varphi\Rightarrow\Gamma\vdash_{B_\mathbb{R}}\varphi.

Beweis:

1. Variante: verallgemeinere den Beweis von Korrektheitslemma und Korrektheitssatz für B auf B_\mathbb{R} (Problem: wir haben mehrfach ausgenutzt, dass B=\{0,1\} mit 0<1)
2. Variante: Folgerung aus Korrektheitssatz für B.

Korollar: Jedes Theorem ist eine $B_\mathbb{R}$-Tautologie.

Korrektheitslemma für nat. Schließen & Wahrheitswertebereich H_{mathbb{R}}

Sei D eine Deduktion mit Hypothesen in der Menge \Gamma und Konklusion \varphi, die die Regel (raa) nicht verwendet. Dann gilt \Gamma\vdash_{H_\mathbb{R}}\varphi.

Beweis: ähnlich zum Beweis des Korrektheitslemmas für den Wahrheitswertebereich B. Nur die Behandlung der Regel (raa) kann nicht übertragen werden.

Beispiel: Sei p eine atomare Formel. 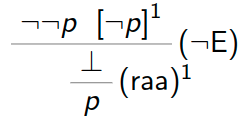Also gilt \{\lnot\lnot p\}\vdash p, d.h. p ist syntaktische Folgerung von \lnot\lnot p.

• Sei B $H_{mathbb{R}}$-Belegung mit B(p)=\mathbb{R}\backslash\{0\}.
• \Rightarrow B(\lnot\lnot p) =\mathbb{R}\not\subseteq \mathbb{R}\backslash\{0\}=B(p)
• \Rightarrow\lnot\lnot p\not\Vdash_{H_{mathbb{R}}} p, d.h. p ist keine H_{mathbb{R}} -Folgerung von \lnot\lnot p.

Korrektheitssatz für nat. Schließen & Wahrheitswertebereich H_{mathbb{R}}

Für jede Menge von Formeln \Gamma und jede Formel \varphi gilt \Gamma\vdash\varphi ohne (raa) \Rightarrow\Gamma\vdash_{H_{mathbb{R}}}\varphi.

Korollar: Jedes $(raa)$-frei herleitbare Theorem ist eine $H_{mathbb{R}}$-Tautologie.

Folgerung: Jede Deduktion der Theoreme \lnot\lnot\varphi\rightarrow\varphi und \varphi\vee\lnot\varphi ohne Hypothesen verwendet (raa).

Vollständigkeit

Können wir durch mathematische Beweise zu allen korrekten Aussagen kommen?

Können wir durch das natürliche Schließen zu allen korrekten Aussagen kommen?

Existiert eine Menge \Gamma von Formeln und eine Formel \varphi mit \Gamma\vdash_W\varphi und \Gamma\not\vdash\varphi? Für welche Wahrheitswertebereiche W?

Frage für diese Vorlesung: Für welche Wahrheitswertebereiche W gilt \Gamma\vdash_W \varphi\Rightarrow\Gamma\vdash\varphi bzw. \varphi ist $W$-Tautologie \Rightarrow\varphi ist Theorem?

Plan

• Sei W einer der Wahrheitswertebereiche B,K_3 ,F ,B_\mathbb{R}, H_{mathbb{R}}.
• z.z. ist \Gamma\vdash_W\varphi\Rightarrow\Gamma\vdash\varphi.
• dies ist äquivalent zu \Gamma\not\vdash\varphi\Rightarrow\Gamma\not\Vdash_W \varphi.
• hierzu gehen wir folgendermaßen vor:
  • \Gamma \not\Vdash_W\varphi
  • \Leftrightarrow \Gamma\cup\{\lnot\varphi\} konsistent
  • \Rightarrow \exists\Delta\subseteq\Gamma\cup\{\lnot\varphi\} maximal konsistent
  • \Rightarrow \Delta erfüllbar
  • \Rightarrow \Gamma\cup\{\lnot\varphi\} erfüllbar
  • \Leftrightarrow \Gamma\not\Vdash_B \varphi
  • \Rightarrow \Gamma\not\Vdash\varphi

Konsistente Mengen

Definition

Sei \Gamma eine Menge von Formeln. \Gamma heißt inkonsistent, wenn \Gamma\vdash\bot gilt. Sonst heißt \Gamma konsistent.

Lemma

Sei \Gamma eine Menge von Formeln und \varphi eine Formel. Dann gilt \Gamma\not\vdash\varphi \Leftrightarrow \Gamma\cup\{\lnot\varphi\} konsistent.

Beweis: Wir zeigen „\Gamma\vdash\varphi\Leftrightarrow \Gamma\cup\{\lnot\varphi\} inkonsistent“:

• Richtung „$\Rightarrow$“, gelte also \Gamma \vdash \varphi.
  • \Rightarrow es gibt Deduktion D mit Hypothesen in \Gamma und Konklusion \varphi
  • \Rightarrow Wir erhalten die folgende Deduktion mit Hypothesen in \Gamma\cup\{\lnot\varphi\} und Konklusion \bot: \frac{\lnot\varphi\quad\varphi}{\bot}
  • \Rightarrow\Gamma\cup\{\lnot\varphi\}\vdash\bot, d.h.$\Gamma\cup{\lnot\varphi}$ ist inkonsistent.
• Richtung „$\Leftarrow$“, sei also \Gamma\cup\{\lnot\varphi\} inkonsistent.
  • \Rightarrow Es gibt Deduktion D mit Hypothesen in \Gamma\cup\{\lnot\varphi\} und Konklusion \bot.
  • \Rightarrow Wir erhalten die folgende Deduktion mit Hypothesen in \Gamma und Konklusion \varphi: \frac{\bot}{\varphi}
  • \Gamma\vdash\varphi

Maximal konsistente Mengen

Definition

Eine Formelmenge \Delta ist maximal konsistent, wenn sie konsistent ist und wenn gilt „\sum\supseteq\Delta konsistent $\Rightarrow\sum = \Delta$“.

Satz

Jede konsistente Formelmenge \Gamma ist in einer maximal konsistenten Formelmenge \Delta enthalten.

Beweis: Sei \varphi_1,\varphi_2,... eine Liste aller Formeln (da wir abzählbar viele atomare Formeln haben, gibt es nur abzählbar viele Formeln)

Wir definieren induktiv konsistente Mengen \Gamma_n:

• Setze \Gamma_1 = \Gamma
• Setze \Gamma_{n+1}= \begin{cases} \Gamma_n\cup\{\varphi_n\}\quad\text{ falls diese Menge konsistent} \\ \Gamma_n \quad\text{sonst}\end{cases}

Setze nun \Delta =\bigcup_{n\geq 1} \Gamma_n.

1. Wir zeigen indirekt, dass \Delta konsistent ist: Angenommen, \Delta\vdash\bot.
   • \Rightarrow Es gibt Deduktion D mit Konklusion \bot und endlicher Menge von Hypothesen \Delta'\subseteq\Delta.
   • \Rightarrow Es gibt n\geq 1 mit \Delta'\subseteq\Gamma_n
   • \Rightarrow \Gamma_n\vdash\bot, zu \Gamma_n konsistent. Also ist \Delta konsistent.
2. Wir zeigen indirekt, dass \Delta maximal konsistent ist. Sei also \sum\supseteq\Delta konsistent. Angenommen, \sum\not=\Delta.
   • \Rightarrow es gibt n\in N mit \varphi_n\in\sum\backslash\Delta
   • \Rightarrow \Gamma_n\cup\{\varphi_n\}\subseteq\Delta\cup\sum= \sum konsistent.
   • \Rightarrow \varphi_n \in\Gamma_{n+1}\subseteq \Delta, ein Widerspruch, d.h. \Delta ist max. konsistent.

Lemma 1

Sei \Delta maximal konsistent und gelte \Delta\vdash\varphi. Dann gilt \varphi\in\Delta.

Beweis:

1. Zunächst zeigen wir indirekt, dass \Delta\cup\{\varphi\} konsistent ist:

   • Angenommen, \Delta\cup\{\varphi\}\vdash\bot.
   • \Rightarrow \exists Deduktion D mit Hypothesen in \Delta\cup\{\varphi\} und Konklusion \bot.
   • \Delta\vdash \varphi \Rightarrow \exists Deduktion E mit Hypothesen in \Delta und Konklusion \varphi.
   • \Rightarrow Wir erhalten die folgende Deduktion: \frac{\Delta \frac{\Delta}{\varphi}}{\bot}

   Also \Delta\vdash\bot, ein Widerspruch zur Konsistenz von \Delta. Also ist \Delta\cup\{\varphi\} konsistent.

2. Da \Delta\cup\{\varphi\}\supseteq\Delta konsistent und \Delta maximal konsistent ist, folgt \Delta=\Delta\cup\{\varphi\}, d.h. \varphi\in\Delta.

Lemma 2

Sei \Delta maximal konsistent und \varphi Formel. Dann gilt \varphi\not\in\Delta\Leftrightarrow\lnot\varphi\in\Delta.

Beweis:

• Zunächst gelte \lnot\varphi\in\Delta. Angenommen, \varphi\in\Delta. Dann haben wir die Deduktion \frac{\lnot\varphi\quad\varphi}{\bot} und damit \Delta\vdash\bot, was der Konsistenz von \Delta widerspricht.
• Gelte nun \varphi\not\in\Delta.
  • \Rightarrow \Delta(\Delta\cup\{\varphi\}\Rightarrow\Delta\cup\{\varphi\} inkonsistent (da \Delta max. konsistent)
  • \Rightarrow Es gibt Deduktion D mit Hypothesen in \Delta\cup\{\varphi\} &Konklusion \bot.
  • \Rightarrow Wir erhalten die folgende Deduktion: \frac{\bot}{\lnot\varphi}
  • \Rightarrow \Delta\vdash\lnot\varphi\Rightarrow\lnot\varphi\in\Delta (nach Lemma 1)

Erfüllbare Mengen

Definition

Sei \Gamma eine Menge von Formeln. \Gamma heißt erfüllbar, wenn es eine passende B-Belegung B gibt mit B(\gamma) = 1_B für alle \gamma\in\Gamma.

Bemerkung

• Die Erfüllbarkeit einer endlichen Menge \Gamma ist entscheidbar:
  • Berechne Menge V von in \Gamma vorkommenden atomaren Formeln
  • Probiere alle B-Belegungen B:V\rightarrow B durch
• Die Erfüllbarkeit einer endlichen Menge \Gamma ist NP-vollständig (Satz von Cook)

Satz Sei \Delta eine maximal konsistente Menge von Formeln. Dann ist \Delta erfüllbar.

Beweis: Definiere eine B-Belegung B mittels $B(p_i) = \begin{cases} 1_B \quad\text{ falls } p_i\in\Delta \ 0_B \quad\text{ sonst. } \end{cases}$ Wir zeigen für alle Formeln \varphi: B(\varphi) = 1_B \Leftarrow\Rightarrow\varphi\in\Delta (*)

Der Beweis erfolgt per Induktion über die Länge von \varphi.

1. I.A.: hat \varphi die Länge 1, so ist \varphi atomare Formel. Hier gilt (*) nach Konstruktion von B.

2. I.V.: Gelte (*) für alle Formeln der Länge <n.

3. I.S.: Sei \varphi Formel der Längen$>1$. \Rightarrow Es gibt Formeln \alpha und \beta der Länge$<n$ mit \varphi\in\{\lnot\alpha,\alpha\wedge\beta,\alpha\vee\beta,\alpha\rightarrow\beta\}.

   • Wir zeigen (*) für diese vier Fälle einzeln auf den folgenden Folien.
   • Zur Erinnerung: \Delta max. konsistent, \varphi Formel
     • Lemma 1: \Delta\vdash\varphi\Rightarrow\varphi\in\Delta
     • Lemma 2: \varphi\not\in\Delta\Leftarrow\Rightarrow\lnot\varphi\in\Delta

4. \varphi =\lnot\alpha. B(\varphi) = 1_B \Leftarrow\Rightarrow B(\alpha) = 0_B \Leftarrow\Rightarrow \alpha\not\in\Delta\Leftarrow\Rightarrow \Delta \owns\lnot\alpha =\varphi

5. \varphi =\alpha\wedge\beta.

• B(\varphi) = 1_B \Rightarrow B(\alpha) =B(\beta) = 1_B \Rightarrow\alpha,\beta\in\Delta\Rightarrow\Delta\vdash\varphi denn \frac{\alpha\quad\beta}{\alpha\wedge\beta} ist Deduktion \Rightarrow\varphi\in\Delta.
• \varphi \in \Delta \Rightarrow\Delta\vdash\alpha und \Delta\vdash\beta denn \frac{\varphi}{\alpha} und \frac{\varphi}{\beta} sind Deduktionen. \Rightarrow\alpha,\beta\in\Delta\Rightarrow B(\alpha),B(\beta) = 1_B=\Rightarrow B(\varphi) = 1_B

3. \varphi =\alpha\vee\beta.

• B(\varphi) = 1_B \Rightarrow B(\alpha) = 1_B oder B(\beta) = 1_B
  • angenommen, B(\alpha) = 1_B \Rightarrow\alpha\in\Delta\Rightarrow\Delta\vdash\varphi denn \frac{\alpha}{\varphi} ist Deduktion \Rightarrow\varphi\in\Delta
  • angenommen, B(\alpha) = 0_B \Rightarrow B(\beta) = 1_B. weiter analog.
• \varphi\in\Delta. Dann gilt \Delta\cup\{\lnot\alpha ,\lnot\beta\}\vdash \bot aufgrund der Deduktion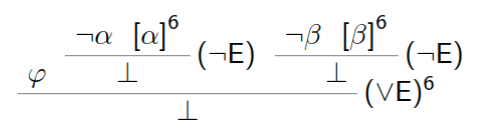 Da \Delta konsistent ist, folgt \Delta\not=\Delta\cup\{\lnot\alpha,\lnot\beta\} und damit \lnot\alpha\in\Delta oder \lnot\beta\in\Delta. \Rightarrow\alpha\in\Delta oder \beta\in\Delta nach Lemma 2 \Rightarrow B(\alpha) = 1_B oder $B(\beta) =1_B$ \Rightarrow B(\varphi) = 1_B.

4. \varphi = \alpha\rightarrow\beta.

• B(\varphi) = 1_B \Rightarrow B(\alpha) = 0_B oder B(\beta) = 1_B \Rightarrow\lnot\alpha\in\Delta oder $\beta\in\Delta$ Aufgrund nebenstehender Deduktionen gilt in beiden Fällen $\Delta\vdash\alpha\rightarrow\beta\Rightarrow\varphi\in\Delta$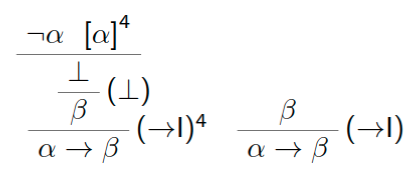
• \varphi\in\Delta. Angenommen, B(\varphi) = 0_B = \Rightarrow B(\alpha) = 1_B, B(\beta) = 0_B $\Rightarrow\alpha\in\Delta, \beta\not\in\Delta \Rightarrow \lnot\beta\in\Delta$ Aufgrund der nebenstehenden Deduktion gilt \Delta\vdash\bot, d.h. \Delta ist inkonsistent, im Widerspruch zur Annahme. $\Rightarrow B(\varphi) = 1_B$

Lemma

Sei \Gamma eine Menge von Formeln und \varphi eine Formel. Dann gilt \Gamma\not\Vdash_B\varphi\Leftarrow\Rightarrow\Gamma\cup\{\lnot \varphi\} erfüllbar.

Beweis: \Gamma\not\Vdash_B\varphi \Leftarrow\Rightarrow es gibt passende B-Belegung B mit $inf{B(\gamma)|\gamma\in\Gamma} \not\leq_B B(\varphi)$ \Leftarrow\Rightarrow es gibt passende B-Belegung B mit inf\{B(\gamma)|\gamma\in\Gamma\}= 1_B und $B(\varphi)=0_B$ \Leftarrow\Rightarrow es gibt passende B-Belegung B mit B(\gamma) = 1_B für alle \gamma\in\Gamma und $B(\lnot\varphi) = 1_B$ \Leftarrow\Rightarrow \Gamma\cup\{\lnot\varphi\} erfüllbar

Beobachtung: Sei W einer der Wahrheitswertebereiche B, K_3, F, H_R und B_R,\Gamma eine Menge von Formeln und \varphi eine Formel. Dann gilt \Gamma\Vdash W\varphi\Rightarrow\Gamma\Vdash B\varphi.

Beweis: Sei B beliebige B-Belegung, die zu jeder Formel in \Gamma\cup\{\varphi\} paßt. definiere W-Belegung B_W durch B_W(pi) = \begin{cases} 1_W \quad\text{ falls } B(p_i) = 1_B \\ 0_W \quad\text{ sonst} \end{cases}. per Induktion über die Formelgröße kann man für alle Formeln \psi, zu denen B paßt, zeigen: B_W(\psi) = \begin{cases} 1_W \quad\text{ falls } B(\psi) = 1_B \\ 0_W \quad\text{ sonst.} \end{cases} (*)

Wir unterscheiden zwei Fälle:

• inf\{B(\gamma)|\gamma\in\Gamma\}= 1_B \Rightarrow inf\{B_W(\gamma)|\gamma\in\Gamma\} = 1_W (wegen ()) \Rightarrow 1_W = B_W(\varphi) (wegen \Gamma\Vdash_W\varphi) \Rightarrow 1_B = B(\varphi) (wegen ()) \Rightarrow inf\{B(\gamma)|\gamma\in\Gamma\} = 1_B \leq B(\varphi) und
• $inf{B(\gamma)|\gamma\in\Gamma} \not= 1_B \Rightarrow inf{B(\gamma)|\gamma\in\Gamma}= 0_B$ \Rightarrow inf\{B(\gamma)|\gamma\in\Gamma\}= 0_B \leq B(\varphi).

Da B beliebig war, gilt \Gamma\Vdash_B \varphi.

Satz (Vollständigkeitssatz)

Sei \Gamma eine Menge von Formeln, \varphi eine Formel und W einer der Wahrheitswertebereiche B,K_3 , F, B_R und H_R. Dann gilt \Gamma\Vdash_W\varphi \Rightarrow \Gamma\vdash\varphi. Insbesondere ist jede W-Tautologie ein Theorem.

Beweis: indirekt

• \Gamma\not\Vdash
• \Gamma\cup\{\lnot\varphi\} konsistent
• \exists\Delta\supseteq\Gamma\cup\{\lnot\varphi\} maximal konsistent
• \Rightarrow\Delta erfüllbar
• \Gamma\cup\{\lnot\varphi\} erfüllbar
• \Gamma\not\Vdash_B \varphi
• \Gamma\not\Vdash_W \varphi

Vollständigkeit und Korrektheit

Satz

Seien \Gamma eine Menge von Formeln und \varphi eine Formel. Dann gilt \Gamma\vdash\varphi\Leftarrow\Rightarrow\Gamma\Vdash_B \varphi. Insbesondere ist eine Formel genau dann eine B-Tautologie, wenn sie ein Theorem ist.

Beweis: Folgt unmittelbar aus Korrektheitssatz und Vollständigkeitssatz.

Bemerkung:

• gilt für jede „Boolesche Algebra“, z.B. B_R
• \Gamma\vdash\varphi ohne (raa) \Leftarrow\Rightarrow\Gamma\Vdash_{H_R} \varphi (Tarksi 1938)

Folgerung 1: Entscheidbarkeit

Satz: die Menge der Theoreme ist entscheidbar.

Beweis: Sei \varphi Formel und V die Menge der vorkommenden atomaren Formeln. Dann gilt \varphi Theorem

• \Leftarrow\Rightarrow\varphi B-Tautologie
• \Leftarrow\Rightarrow für alle Abbildungen B:V\rightarrow\{0_B, 1_B\} gilt B(\varphi) = 1_B

Da es nur endlich viele solche Abbildungen gibt und B(\varphi) berechnet werden kann, ist dies eine entscheidbare Aussage.

Folgerung 2: Äquivalenzen und Theoreme

Definition

Zwei Formeln \alpha und \beta heißen äquivalent (\alpha\equiv\beta), wenn für alle passenden B-Belegungen B gilt: B(\alpha) =B(\beta).

Satz: Es gelten die folgenden Äquivalenzen:

1. p_1 \vee p_2 \equiv p_2 \vee p_1
2. (p_1 \vee p_2 )\vee p_3 \equiv p_1 \vee (p_2 \vee p_3 )
3. p_1 \vee (p_2 \wedge p_3 )\equiv (p_1 \vee p_2 )\wedge (p_1 \vee p_3 )
4. \lnot(p_1 \vee p_2 )\equiv\lnot p_1 \wedge\lnot p_2
5. p_1 \vee p_1 \equiv p_1
6. (p_1 \wedge \lnot p_1 )\vee p_2 \equiv p_2
7. \lnot\lnot p_1\equiv p_1
8. p_1 \wedge\lnot p_1 \equiv\bot
9. p_1 \vee\lnot p_1 \equiv\lnot\bot
10. p_1 \rightarrow p_2 \equiv \lnot p_1 \vee p_2

Beweis: Wir zeigen nur die Äquivalenz (3): Sei B beliebige B-Belegung, die wenigstens auf \{p_1, p_2, p_3\} definiert ist. Dazu betrachten wir die Wertetabelle:

B(p_1)	B(p_2)	B(p_3)	B(p_1\vee(p_2\wedge p_3))	B((p_1\vee p_2)\wedge(p_1 \vee p_3 ))
0_B	0_B	0_B	0_B	0_B
0_B	0_B	1_B	0_B	0_B
0_B	1_B	0_B	0_B	0_B
0_B	1_B	1_B	1_B	1_B
1_B	0_B	0_B	1_B	1_B
1_B	0_B	1_B	1_B	1_B
1_B	1_B	0_B	1_B	1_B
1_B	1_B	1_B	1_B	1_B

Die anderen Äquivalenzen werden analog bewiesen.

Aus dieser Liste von Äquivalenzen können weitere hergeleitet werden:

Beispiel: Für alle Formeln \alpha und \beta gilt \lnot(\alpha\wedge\beta)\equiv\lnot\alpha\vee\lnot\beta.

Beweis: \lnot(\alpha\wedge\beta) \equiv \lnot(\lnot\lnot\alpha\wedge\lnot\lnot\beta) \equiv \lnot\lnot(\lnot\alpha\vee\lnot\beta) \equiv \lnot\alpha\vee\lnot\beta

Bemerkung Mit den üblichen Rechenregeln für Gleichungen können aus dieser Liste alle gültigen Äquivalenzen hergeleitet werden.

Zusammenhang zw. Theoremen und Äquivalenzen

Satz

Seien \alpha und \beta zwei Formeln. Dann gilt \alpha\equiv\beta\Leftarrow\Rightarrow(\alpha\leftrightarrow\beta) ist Theorem.

Beweis: \alpha\equiv\beta

• \Leftarrow\Rightarrow für alle passenden B-Belegungen B gilt B(\alpha)=B(\beta)
• \Leftarrow\Rightarrow \{\alpha\}\Vdash_B\beta und \{\beta\}\Vdash_B \alpha
• \Leftarrow\Rightarrow \{\alpha\}\vdash\beta und \{\beta\}\vdash\alpha (nach Korrektheits- und Vollständigkeitssatz)

es bleibt z.z., dass dies äquivalent zu \varnothing\vdash(\alpha\leftrightarrow\beta) ist.

• \Rightarrow: Wir haben also Deduktionen mit Hypothesen in \{\alpha\} bzw. in \{\beta\} und Konklusionen \beta bzw.$\alpha$. Es ergibt sich eine hypothesenlose Deduktion von \alpha\leftrightarrow\beta:
• \Leftarrow: Wir haben also eine hypothesenlose Deduktion von \alpha\leftrightarrow\beta. Es ergeben sich die folgenden Deduktionen mit Hypothesen \beta bzw. \alpha und Konklusionen \alpha bzw. \beta: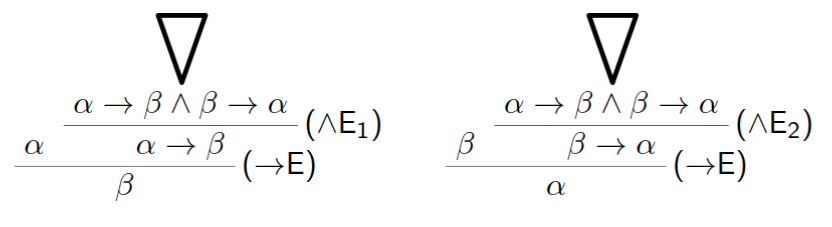

Satz

Sei \alpha eine Formel. Dann gilt \alpha ist Theorem \Leftarrow\Rightarrow\alpha\equiv\lnot\bot.

Beweis: \alpha ist Theorem

• \Leftarrow\Rightarrow\alpha ist B-Tautologie (Korrektheits- und Vollständigkeitssatz)
• \Leftarrow\Rightarrow für alle passenden B-Belegungen B gilt B(\alpha) = 1_B
• \Leftarrow\Rightarrow für alle passenden B-Belegungen B gilt B(\alpha) =B(\lnot\bot)
• \Leftarrow\Rightarrow\alpha\equiv\lnot\bot

Folgerung 3: Kompaktheit

Satz

Sei \Gamma eine u.U. unendliche Menge von Formeln und \varphi eine Formel mit \Gamma\Vdash_B\varphi. Dann existiert \Gamma′\subseteq\Gamma endlich mit \Gamma′\Vdash_B \varphi.

Beweis: \Gamma\Vdash_B\varphi

• \Rightarrow\Gamma\vdash\varphi (nach dem Vollständigkeitssatz)
• \Rightarrow es gibt Deduktion von \varphi mit Hypothesen \gamma_1,...,\gamma_n\in\Gamma
• \Rightarrow\Gamma′=\{\gamma_1,...,\gamma_n\}\subseteq\Gamma endlich mit \Gamma′\vdash\varphi
• \Rightarrow\Gamma′\Vdash_B\varphi (nach dem Korrektheitssatz).

Folgerung (Kompaktheits- oder Endlichkeitssatz)

Sei \Gamma eine u.U. unendliche Menge von Formeln. Dann gilt \Gamma unerfüllbar \Leftarrow\Rightarrow\exists\Gamma′\subseteq\Gamma endlich: \Gamma′ unerfüllbar

Beweis: \Gamma unerfüllbar

• \Leftarrow\Rightarrow\Gamma\cup\{\lnot\bot\} unerfüllbar
• \Leftarrow\Rightarrow\Gamma\Vdash_B\bot
• \Leftarrow\Rightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′\Vdash_B\bot
• \Leftarrow\Rightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′\cup\{\lnot\bot\} unerfüllbar
• \Leftarrow\Rightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′ unerfüllbar

1. Anwendung des Kompaktheitsatzes: Färbbarkeit

Definition

Ein Graph ist ein Paar G=(V,E) mit einer Menge V und $E\subseteq\binom{V}{2} ={X\subseteq V:|V$\Vdash$ 2 }$. Für W\subseteq V sei G\upharpoonright_W= (W,E\cap\binom{W}{2}) der von W induzierte Teilgraph. Der Graph G ist 3-färbbar, wenn es eine Abbildung f:V\rightarrow\{1,2,3\} mit f(v)\not=f(w) für alle \{v,w\}\in E.

Bemerkung: Die 3-Färbbarkeit eines endlichen Graphen ist NP-vollständig

Satz Sei G= (N,E) ein Graph. Dann sind äquivalent

1. G ist 3-färbbar.
2. Für jede endliche Menge W\subseteq N ist G\upharpoonright_W 3-färbbar.

Beweis:

• 1.\Rightarrow 2. trivial
• 2.\Rightarrow 1. Sei nun, für alle endlichen Menge W\subseteq N, der induzierte Teilgraph G\upharpoonright_W 3-färbbar.

Wir beschreiben zunächst mit einer unendlichen Menge \Gamma von Formeln, dass eine 3-Färbung existiert:

• atomare Formeln p_{n,c} für n\in N und c\in\{1,2,3\} (Idee: der Knoten n hat die Farbe c)
• \Gamma enthält die folgenden Formeln:
  • für alle n\in N:p_{n, 1} \vee p_{n, 2} \vee p_{n, 3} (der Knoten n ist gefärbt)
  • für alle n\in N:\bigwedge_{1\leq c< d \leq 3} \lnot(p_{n,c} \wedge p_{n,d}) (der Knoten n ist nur mit einer Farbe gefärbt)
  • für alle \{m,n\}\in E: \bigwedge_{1\leq c\leq 3} \lnot(p_{m,c} \wedge p_{n,c}) (verbundene Knoten m und n sind verschieden gefärbt)

Behauptung: Jede endliche Menge \Delta\subseteq\Gamma ist erfüllbar.

Begründung:

• Da \Delta endlich ist, existiert endliche Menge W\subseteq N, so dass jede atomare Formel in \Delta die Form p_{n,c} für ein n\in W und ein c\in\{1,2,3\} hat.
• Nach Annahme existiert f_W:W\rightarrow\{1,2,3\} mit f_W(m) \not=f(n) f.a. \{m,n\}\in E\cap\binom{W}{2}.
• Definiere B:\{p_{n,c}|n\in W, 1 \leq c\leq 3\}\rightarrow\{0,1\} durch B(p_{n,c}) = \begin{cases} 1 \quad\text{ falls } f_W(n) = c \\ 0 \quad\text{ sonst.} \end{cases}
• Diese Belegung erfüllt \Delta, d.h. \Delta ist erfüllbar, womit die Behauptung gezeigt ist.

Nach dem Kompaktheitssatz ist also \Gamma erfüllbar. Sei B erfüllende Belegung. Für n\in N existiert genau ein c\in\{1,2,3\} mit B(p_{n,c}) =1. Setze f(n) =c. Dann ist f eine gültige Färbung des Graphen G.

2. Anwendung des Kompaktheitsatzes: Parkettierungen

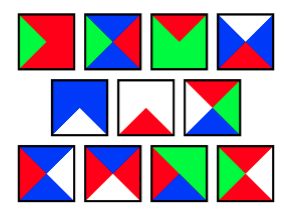
Idee: Gegeben ist eine Menge von quadratischen Kacheln mit gefärbten Kanten. Ist es möglich, mit diesen Kacheln die gesamte Ebene zu füllen,so dass aneinanderstoßende Kanten gleichfarbig sind?

Berühmtes Beispiel: Mit diesen 11 Kacheln kann die Ebene gefüllt werden, aber dies ist nicht periodisch möglich.

Definition

Ein Kachelsystem besteht aus einer endlichen Menge C von „Farben“ und einer Menge K von Abbildungen \{N,O,S,W\}\rightarrow C von „Kacheln“. Eine Kachelung von G\subseteq Z\times Z ist eine Abbildung f:G\rightarrow K mit

• f(i,j)(N) =f(i,j+ 1 )(S) für alle (i,j),(i,j+ 1 )\in G
• f(i,j)(O) =f(i+ 1 ,j)(W) für alle (i,j),(i+ 1 ,j)\in G

Satz

Sei K ein Kachelsystem. Es existiert genau dann eine Kachelung von Z\times Z, wenn für jedes n\in N eine Kachelung von \{(i,j) :|i|,|j| \leq n\} existiert.

Beweis:

• \Rightarrow: trivial
• \Leftarrow: Wir beschreiben zunächst mit einer unendlichen Menge \Gamma von Formeln, dass eine Kachelung existiert: atomare Formeln p_{k,i,j} für k\in K und i,j\in Z (Idee: an der Stelle (i,j) liegt die Kachel k, d.h. f(i,j) =k) Für alle (i,j)\in Z enthält \Gamma die folgenden Formeln:
  • eine der Kacheln aus K liegt an der Stelle (i,j):\bigvee_{k\in K} p_{k,i,j}
  • es liegen nicht zwei verschiedene Kacheln an der Stelle (i,j): \bigwedge_{k,k′\in K,k\not=k′} \lnot(p_{k,i,j}\wedge p_{k′,i,j})
  • Kacheln an Stellen (i,j) und (i,j+1) „passen übereinander“: \bigvee_{k,k′\in K,k(N)=k′(S)} (p_{k,i,j}\wedge p_{k′,i,j+1})
  • Kacheln an Stellen (i,j) und (i+1,j) „passen nebeneinander“: \bigvee_{k,k′\in K,k(W)=k′(O)} (p_{k,i,j}\wedge p_{k′,i+1,j})

Sei nun \Delta\subseteq\Gamma endlich.

• \Rightarrow es gibt n\in N, so dass \Delta nur atomare Formeln der Form p_{k,i,j} mit |i|,|j|\leq n enthält.
• Voraussetzung \Rightarrow es gibt Kachelung g:\{(i,j) :|i|,|j| \leq n\}\rightarrow K für k\in K und |i|,|j|\leq n definiere B(p_{k,i,j}) = \begin{cases} 1_B \quad\text{ falls } g(i,j) =k \\ 0_B \quad\text{ sonst} \end{cases}
• \Rightarrow B(\sigma) = 1_B für alle \sigma\in\Delta (da g Kachelung)
• Also haben wir gezeigt, dass jede endliche Teilmenge von \Gamma erfüllbar ist.
• Kompaktheitssatz \Rightarrow es gibt B-Belegung B mit B(\gamma) = 1_B für alle \gamma\in\Gamma
• \Rightarrow es gibt Abbildung f:Z\times Z\rightarrow K mit f(i,j) =k \Leftarrow\Rightarrow B(p_{k,i,j}) = 1_B.
• Wegen B\Vdash\Gamma ist dies eine Kachelung.

Weitere Anwendungen des Kompaktheitsatzes

• abz. partielle Ordnungen sind linearisierbar
• abz. Gleichungssystem über \mathbb{Z}_2 lösbar \Leftarrow\Rightarrow jedes endliche Teilsystem lösbar
• Heiratsproblem
• Kőnigs Lemma (Übung)
• ...

Bemerkung: Der Kompaktheitssatz gilt auch, wenn die Menge der atomaren Formeln nicht abzählbar ist. Damit gelten die obigen Aussagen allgemeiner:

• 3-Färbbarkeit: beliebige Graphen
• Linearisierbarkeit: beliebige partielle Ordnungen
• Lösbarkeit: beliebig große Gleichungssysteme über \mathbb{Z}_2
• ...

Erfüllbarkeit

Erfüllbarkeitsproblem

Eingabe: Formel \Gamma

Frage: existiert eine B-Belegung B mit B(\Gamma) = 1_B.

• offensichtlicher Algorithmus: probiere alle Belegungen durch (d.h. stelle Wahrheitswertetabelle auf)\rightarrow exponentielle Zeit
• „Automaten, Sprachen und Komplexität“: das Problem ist NP-vollständig
• nächstes Ziel:spezielle Algorithmen für syntaktisch eingeschränkte Formeln \Gamma
• Spätere Verallgemeinerung dieser Algorithmen (letzte Vorlesung des Logik-Teils von „Logik und Logikprogrammierung“) bildet Grundlage der logischen Programmierung.

Hornformeln (Alfred Horn, 1918–2001)

Definition

Eine Hornklausel hat die Form (\lnot\bot\wedge p_1\wedge p_2\wedge ... \wedge p_n)\rightarrow q für n\geq 0, atomare Formeln p_1 ,p_2 ,... ,p_n und q atomare Formel oder q=\bot. Eine Hornformel ist eine Konjunktion von Hornklauseln.

Schreib- und Sprechweise

• \{p_1,p_2 ,... ,p_n\}\rightarrow q für Hornklausel $(\lnot\bot\wedge p_1 \wedge p_2 \wedge ...\wedge p_n)\rightarrow q$ insbes. \varnothing\rightarrow q für \lnot\bot\rightarrow q
• \{(M_i\rightarrow q_i)| 1 \leq i\leq n\} für Hornformel \bigwedge_{1 \leq i \leq n} (M_i\rightarrow q_i)

Bemerkung, in der Literatur auch:

• \{\lnot p_1,\lnot p_2 ,... ,\lnot p_n,q\} für \{p_1 ,... ,p_n\}\rightarrow q mit q atomare Formel
• \{\lnot p_1,\lnot p_2 ,... ,\lnot p_n\} für \{p_1 ,... ,p_n\}\rightarrow\bot
• \Box für \varnothing\rightarrow\bot, die „leere Hornklausel“

Markierungsalgorithmus

• Eingabe: eine endliche Menge \Gamma von Hornklauseln.

1. while es gibt in \Gamma eine Hornklausel M\rightarrow q, so dass alle p\in M markiert sind und q unmarkierte atomare Formel ist: do markiere q (in allen Hornklauseln in \Gamma)
2. if \Gamma enthält eine Hornklausel der Form M\rightarrow\bot, in der alle p\in M markiert sind then return „unerfüllbar“ else return „erfüllbar“

Beweis einer Folgerung: Beispiel

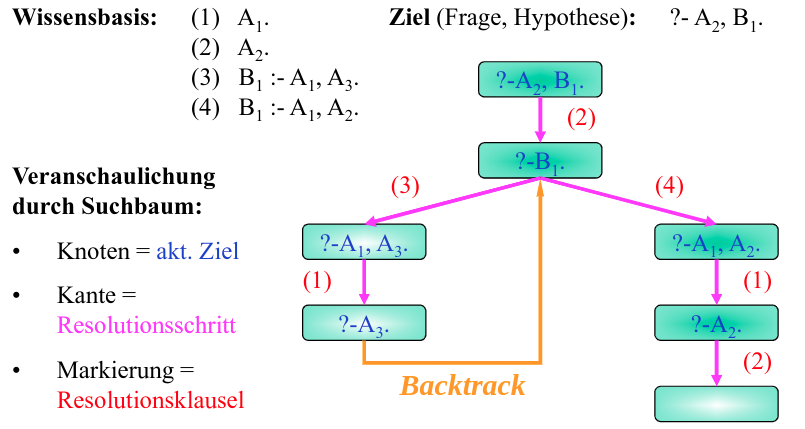
• Ziel ist es, die folgende Folgerung zu zeigen: \{(AK\vee BK),(AK\rightarrow BK),(BK\wedge RL\rightarrow\lnot AK),RL\}\Vdash\lnot AK
• Lemma: man muß Unerfüllbarkeit der folgenden Menge zeigen: \{(AK\vee BK),(AK\rightarrow BK),(BK\wedge RL\rightarrow \lnot AK),RL,\lnot\lnot AK\}
• Dies ist keine Menge von Hornklauseln!
• Idee: ersetze BK durch \lnot BH in allen Formeln.
• Ergebnis:
  • Aus AK\vee BK wird \lnot BH\vee AK\equiv BH\rightarrow AK\equiv\{BH\}\rightarrow AK.
  • Aus AK\rightarrow BK wird AK\rightarrow\lnot BH\equiv\lnot AK\vee\lnot BH\equiv AK\wedge BH\rightarrow\bot\equiv\{AK,BH\} \rightarrow\bot.
  • Aus BK\wedge RL\rightarrow\lnot AK wird \lnot BH\wedge RL\rightarrow\lnot AK\equiv BH\vee\lnot RL\vee\lnot AK\equiv RL\wedge AK\rightarrow BH\equiv\{RL,AK\}\rightarrow BH
  • RL\equiv (\varnothing\rightarrow RL)
  • \lnot\lnot AK\equiv (\varnothing\rightarrow AK)
• Wir müssen also zeigen, dass die folgende Menge von Hornklauseln unerfüllbar ist: \{\{BH\}\rightarrow AK,\{AK,BH\}\rightarrow\bot,\{RL,AK\}\rightarrow BH,\varnothing\rightarrow RL,\varnothing\rightarrow AK\}

Der Markierungsalgorithmus geht wie folgt vor:

1. Runde: markiere RL aufgrund der Hornklausel \varnothing\rightarrow RL
2. Runde: markiere AK aufgrund der Hornklausel \varnothing\rightarrow AK
3. Runde: markiere BH aufgrund der Hornklausel \{RL,AK\}\rightarrow BH

dann sind keine weiteren Markierungen möglich.

In der Hornklausel \{AK,BH\}\rightarrow\bot sind alle atomaren Formeln aus \{AK,BH\} markiert. Also gibt der Algorithmus aus, dass die Menge von Hornklauseln nicht erfüllbar ist.

Nach unserer Herleitung folgern wir, dass das Teil A heil ist.

1. Der Algorithmus terminiert: in jedem Durchlauf der while-Schleife wird wenigstens eine atomare Formel markiert. Nach endlich vielen Schritten terminiert die Schleife also.
2. Wenn der Algorithmus eine atomare Formelqmarkiert und wenn B eine B-Belegung ist, die \Gamma erfüllt, dann gilt B(q) = 1_B. Beweis: wir zeigen induktiv über n: Wenn q in einem der ersten n Schleifendurchläufe markiert wird, dann gilt B(q) = 1_B.

• I.A. Die Aussage gilt offensichtlich für n=0.
• I.S. werde die atomare Formel q in einem der ersten n Schleifendurchläufe markiert. Dann gibt es eine Hornklausel \{p_1,p_2 ,... ,p_k\}\rightarrow q, so dass p_1 ,... ,p_k in den ersten n-1 Schleifendurchläufen markiert wurden. Also gilt B(p_1)=...=B(p_k) = 1_B nach IV. Da B alle Hornformeln aus \Gamma erfüllt, gilt insbesondere B(\{p_1 ,p_2 ,... ,p_k\}\rightarrow q) = 1_B und damit B(q) = 1_B.

3. Wenn der Algorithmus „unerfüllbar“ ausgibt, dann ist \Gamma unerfüllbar. Beweis: indirekt, wir nehmen also an, dass der Algorithmus „unerfüllbar“ ausgibt, B aber eine B-Belegung ist, die \Gamma erfüllt. Sei \{p_1 ,... ,p_k\}\rightarrow\bot die Hornklausel aus \Gamma, die die Ausgabe „unerfüllbar“ verursacht (d.h. die atomaren Formeln p_1 ,... ,p_k sind markiert). Nach 2. gilt B(p_1) =...=B(p_k) = 1_B, also B(\{p_1 ,p_2 ,... ,p_k\}\rightarrow\bot) = 0_B im Widerspruch zur Annahme, dass B alle Hornklauseln aus \Gamma erfüllt. Also kann es keine erfüllende B-Belegung von \Gamma geben.
4. Wenn der Algorithmus „erfüllbar“ ausgibt, dann erfüllt die folgende B-Belegung alle Formeln aus \Gamma: $B(p_i)=\begin{cases} 1_B \quad\text{ der Algorithmus markiert } p_i \ 0_B \quad\text{ sonst} \end{cases}$ Beweis:
   • Sei M\rightarrow q eine beliebige Hornklausel aus \Gamma.
   • Ist ein p\in M nicht markiert, so gilt B(\bigwedge_{p\in M} p) = 0_B und damit B(M\rightarrow q) = 1_B.
   • Sind alle p\in M markiert, so wird auch q markiert, also B(q) = 1_B und damit B(M\rightarrow q) = 1_B.
   • Gilt q=\bot, so existiert unmarkiertes p\in M (da der Algorithmus sonst „unerfüllbar“ ausgegeben hätte), also B(M\rightarrow\bot) = 1_B wie im ersten Fall. Also gilt B(M\rightarrow q) = 1_B für alle Hornklauseln aus \Gamma, d.h. \Gamma ist erfüllbar.

Satz

Sei \Gamma endliche Menge von Hornklauseln. Dann terminiert der Markierungsalgorithmus mit dem korrekten Ergebnis.

Beweis: Die Aussagen 1.-4. beweisen diesen Satz.

Bemerkungen:

• Mit einer geeigneten Implementierung läuft der Algorithmusin linearer Zeit.
• Wir haben sogar gezeigt, dass bei Ausgabe von „erfüllbar“ eine erfüllende B-Belegung berechnet werden kann.

SLD-Resolution

Definition

Sei \Gamma eine Menge von Hornklauseln. Eine SLD-Resolution aus \Gamma ist eine Folge (M_0\rightarrow\bot,M_1\rightarrow\bot,... ,M_m\rightarrow\bot) von Hornklauseln mit

• (M_0\rightarrow\bot)\in\Gamma
• für alle 0\leq n<m existiert (N\rightarrow q)\in\Gamma mit q\in M_n und M_{n+1} = M_n\backslash\{q\}\cup N

Beispiel:

• \Gamma =\{\{BH\}\rightarrow AK,\{AK,BH\}\rightarrow\bot,\{RL,AK\}\rightarrow BH,\varnothing\rightarrow RL,\varnothing\rightarrow AK\}
• M_0 =\{AK,BH\}
• M_1 =M_0 \backslash\{BH\}\cup\{RL,AK\}=\{RL,AK\}
• M_2 =M_1 \backslash\{RL\}\cup\varnothing =\{AK\}
• M_3 =M_2 \backslash\{AK\}\cup\varnothing =\varnothing

Lemma A

Sei \Gamma eine (u.U. unendliche) Menge von Hornklauseln und (M_0\rightarrow\bot, M_1\rightarrow\bot,... , M_m\rightarrow\bot) eine SLD-Resolution aus \Gamma mit M_m=\varnothing. Dann ist \Gamma nicht erfüllbar.

Beweis:

• indirekt: angenommen, es gibt B-Belegung B mit B(N\rightarrow q) = 1_B für alle (N\rightarrow q)\in\Gamma.
• Wir zeigen für alle 0\leq n\leq m per Induktion über n: es gibt p\in M_n mit B(p) = 0_B (4)
• I.A.: n=0:(M_0 \rightarrow\bot,...) SLD-Resolution \Rightarrow(M_0\rightarrow\bot)\in\Gamma
  • \Rightarrow B(M_0\rightarrow\bot) = 1_B
  • \Rightarrow es gibt p\in M_0 mit B(p) = 0_B
• I.V.: sei n<m und p\in M_n mit B(p) = 0_B
• I.S.: (... ,M_n\rightarrow\bot,M_{n+ 1}\rightarrow\bot,...) SLD-Resolution \Rightarrow es gibt (N\rightarrow q)\in\Gamma mit M_{n+1} =M_n\backslash\{q\}\cup N und q\in M_n. Zwei Fälle werden unterschieden:
  1. p\not=q: dann gilt p\in M_{n+1} mit B(p) = 0_B
  2. p=q:(N\rightarrow q)\in\Gamma\Rightarrow B(N\rightarrow q) = 1_B es gibt p′\in N\subseteq M_{n+1} mit $B(p′)=0_B$ in jedem der zwei Fälle gilt also (4) für n+1.
• Damit ist der induktive Beweis von (4) abgeschlossen.
• Mit m=n haben wir insbesondere "es gibt p\in M_m mit $B(p) = 0_B$" im Widerspruch zu M_m=\varnothing. Damit ist der indirekte Beweis abgeschlossen.

Lemma B

Sei \Gamma eine (u.U. unendliche) unerfüllbare Menge von Hornklauseln. Dann existiert eine SLD-Resolution (M_0\rightarrow\bot,...,M_m\rightarrow\bot) aus \Gamma mit M_m=\varnothing.

Beweis: Endlichkeitssatz: es gibt \Delta\subseteq\Gamma endlich und unerfüllbar. Bei Eingabe von$\Delta$ terminiert Markierungsalgorithmus mit „unerfüllbar“

• r\geq 0... Anzahl der Runden
• q_i... Atomformel, die in i Runde markiert wird (1\leq i\leq r)

Behauptung: Es gibt m\leq r und SLD-Resolution (M_0\rightarrow\bot,...,M_m\rightarrow\bot) aus \Delta mit M_m=\varnothing und M_n\subseteq\{q_1,q_2,... ,q_{r-n}\} f.a. 0\leq n\leq m. (5)

Beweis der Behauptung: Wir konstruieren die Hornklauseln M_i\rightarrow\bot induktiv:

• I.A.: Da der Markierungsalgorithmus mit „unerfüllbar“ terminiert, existiert eine Hornklausel (M_0\rightarrow\bot)\in\Gamma mit M_0\subseteq\{q_1,... ,q_{r- 0}\}. (M_0\rightarrow\bot) ist SLD-Resolution aus \Delta, die (5) erfüllt.
• I.V.: Sei n\leq r und (M_0\rightarrow\bot,... ,M_n\rightarrow\bot) SLD-Resolution, so dass (5) gilt.
• I.S.: wir betrachten drei Fälle:
  1. Fall M_n=\varnothing: mit m:=n ist Beweis der Beh. abgeschlossen.
  2. Fall n=r: Nach (5) gilt M_n\subseteq\{q_1,...,q_{r-n}\}=\varnothing. Mit m:=n ist der Beweis der Beh. abgeschlossen.
  3. Fall n<r und M_n \not=\varnothing. Sei k maximal mit q_k\in M_n\subseteq\{q_1,q_2,... ,q_{r-n}\}. Also existiert (N\rightarrow q_k)\in\Delta, so dass N\subseteq\{q_1,... ,q_{k-1}\}. Setze M_{n+1}=M_n\backslash\{q_k\}\cup N\subseteq\{q_1,... ,q_{k-1}\}\subseteq\{q_1,...,q_{r-(n+1)}\}.

Damit ist der induktive Beweis der Beh. abgeschlossen, woraus das Lemma unmittelbar folgt.

Satz

Sei \Gamma eine (u.U. unendliche) Menge von Hornklauseln. Dann sind äquivalent:

1. \Gamma ist nicht erfüllbar.
2. Es gibt eine SLD-Resolution (M_0\rightarrow\bot,M_1\rightarrow\bot,... ,M_m\rightarrow\bot) aus \Gamma mit M_m=\varnothing.

Beweis: Folgt unmittelbar aus Lemmata A und B.

Beispiel: \Gamma=\{\{a,b\}\rightarrow\bot,\{a\}\rightarrow c, \{b\}\rightarrow c,\{c\}\rightarrow a,\varnothing\rightarrow b; alle SLD-Resolutionen aus$\Gamma$ kann man durch einen Baum beschreiben:

Die Suche nach einer SLD-Resolution mit M_m=\varnothing kann grundsätzlich auf zwei Arten erfolgen:

• Breitensuche:
  • findet SLD-Resolution mit M_m=\varnothing (falls sie existiert), da Baum endlich verzweigend ist (d.h. die Niveaus sind endlich)
  • hoher Platzbedarf, da ganze Niveaus abgespeichert werden müssen (in einem Binärbaum der Tiefe n kann es Niveaus der Größe 2^n geben)
• Tiefensuche:
  • geringerer Platzbedarf (in einem Binärbaum der Tiefe n hat jeder Ast die Länge \leq n)
  • findet existierende SLD-Resolution mit M_m=\varnothing nicht immer (siehe Beispiel)

Zusammenfassung Aussagenlogik

• Das natürliche Schließen formalisiert die „üblichen“ Argumente in mathematischen Beweisen.
• Unterschiedliche Wahrheitswertebereiche formalisieren unterschiedliche Vorstellungen von „Wahrheit“.
• Das natürliche Schließen ist vollständig und korrekt für den Booleschen Wahrheitswertebereich.
• Der Markierungsalgorithmus und die SLD-Resolution sind praktikable Verfahren, um die Erfüllbarkeit von Hornformeln zu bestimmen.

Kapitel 2: Prädikatenlogik

Beispiel: Graphen Um über diesen Graphen Aussagen in der Aussagenlogik zu machen, verwenden wir Formeln \varphi_{i,j} für 1\leq i,j\leq 9 mit \varphi_{i,j}=\begin{cases} \lnot\bot\quad\text{ falls} (v_i,v_j) Kante\\ \bot\quad\text{ sonst}\end{cases}

• Die aussagenlogische Formel \bigvee_{1\leq i,j\leq 9} \varphi_{i,j} sagt aus, dass der Graph eine Kante enthält.
• Die aussagenlogische Formel \bigwedge_{1\leq i\leq 9} \bigvee_{1\leq j\leq 9} \varphi_{i,j} sagt aus, dass jeder Knoten einen Nachbarn hat
• Die aussagenlogische Formel \bigvee_{1\leq i,j,k\leq 9 verschieden} \varphi_{i,j}\wedge\varphi_{j,k}\wedge\varphi_{k,i} sagt aus, dass der Graph ein Dreieck enthält. Man kann so vorgehen, wenn der Graph bekannt und endlich ist. Sollen analoge Aussagen für einen anderen Graphen gemacht werden, so ist die Kodierungsarbeit zu wiederholen.

Beispiel: Datenbanken

• Im folgenden reden wir über die Studenten und die Lehrenden in Veranstaltungen zur Theoretischen Informatik in diesem Semester. Betrachte die folgenden Aussagen:
  • Jeder ist Student oder wissenschaftlicher Mitarbeiter oder Professor.
  • Dietrich Kuske ist Professor.
  • Kein Student ist Professor.
  • Jeder Student ist jünger als jeder Professor.
  • Es gibt eine Person, die an den Veranstaltungen „Logik und Logikprogrammierung“ und „Algorithmen und Datenstrukturen“ teilnimmt.
  • Es gibt eine Person, die kein wissenschaftlicher Mitarbeiter ist und nicht an beiden Veranstaltungen teilnimmt.
  • Jeder Student ist jünger als die Person, mit der er am besten über Informatik reden kann.
• Um sie in der Aussagenlogik machen zu können, müssen wir atomare Aussagen für „Hans ist Student“, „Otto ist jünger als Ottilie“ usw. einführen. Dies ist nur möglich, wenn
  1. alle involvierten Personen bekannt sind und fest stehen und
  2. es nur endlich viele involvierte Personen gibt.
• Sollen analoge Aussagen für das vorige oder das kommende Jahr gemacht werden, so ist die gesamte Kodierungsarbeit neu zu machen.

Kodierung in einer „Struktur“

• Grundmenge: Die Studenten und die Lehrenden in Veranstaltungen zur Theoretischen Informatik in diesem Sommersemester
• Teilmengen:
  • S(x) „x ist Student“
  • LuLP(x) „x nimmt an der Veranstaltung LuLP teil“
  • AuD(x) „x nimmt an der Veranstaltung AuD teil“
  • Pr(x) „x ist Professor“
  • WM(x) „x ist wissenschaftlicher Mitarbeiter“
• Relationen:
  • J(x,y) „x ist jünger als y“
• Funktion:
  • f(x) ist diejenige Person (aus dem genannten Kreis), mit der x am besten über Informatik reden kann.
• Konstante:
  • dk Dietrich Kuske

Die in der Aussagenlogik nur schwer formulierbaren Aussagen werden nun

• Für alle x gilt S(x)\vee WM(x)\vee Pr(x)
• Pr(dk)
• Für alle x gilt S(x)\rightarrow\lnot Pr(x)
• Für alle x und y gilt (S(x)\wedge Pr(y))\rightarrow J(x,y)
• Es gibt ein x mit LuLP(x)\wedge AuD(x)
• Es gibt ein x mit ((\lnot LuLP(x)\vee\lnot AuD(x))\wedge\lnot WM(x))
• Für alle x gilt S(x)\rightarrow J(x,f(x))

Bemerkung: Diese Formulierungen sind auch brauchbar, wenn die Grundmenge unendlich ist. Sie sind auch unabhängig vom Jahr (im nächsten Jahr können diese Folien wieder verwendet werden).

Ziel

• Wir wollen in der Lage sein, über Sachverhalte in „Strukturen“ (Graphen, Datenbanken, relle Zahlen, Gruppen... ) zu reden.
• Dabei soll es „Relationen“ geben, durch die das Enthaltensein in einer Teilmenge oder Beziehungen zwischen Objekten ausgedrückt werden können (z.B. S(x),J(x,y),... )
• Weiter soll es „Funktionen“ geben, durch die Objekte (oder Tupel von Objekten) auf andere Objekte abgebildet werden (z.B. f)
• Nullstellige Funktionen (ohne Argumente): Konstante (z.B. dk)

Fragen

• Nach welchen Regeln bildet man korrekte Formeln?
• Was ist eine Struktur?
• Wann hat eine Aussage in einer Struktur eine Bedeutung (ist „sinnvoll“)?
• Wann „gilt“ eine Aussage in einer Struktur?
• Gibt es Formeln, die in allen Strukturen gelten?
• Kann man solche Formeln algorithmisch identifizieren? Gibt es einen Beweiskalkül wie das natürliche Schließen oder die SLD-Resolution?
• .........

Syntax der Prädikatenlogik

Formeln machen Aussagen über Strukturen. Dabei hat es keinen Sinn zu fragen, ob eine Formel, die über Studenten etc. redet, im Graphen G gilt.

Definition

Eine Signatur ist ein Tripel \sum=(\Omega, Rel,ar), wobei \Omega und Rel disjunkte Mengen von Funktions- und Relationsnamen sind und ar:\Omega\cup Rel\rightarrow\mathbb{N} eine Abbildung ist.

Beispiel: \Omega=\{f,dk\} mit ar(f) =1,ar(dk)=0 und Rel=\{S,LuLP,AuD,Pr,WM,J\} mit ar(S) =ar(LuLP) =ar(AuD) =ar(Pr) =ar(WM) =1 undar(J) = 2 bilden die Signatur der Datenbank von vorhin.

• typische Funktionsnamen: f, g, a, b... mit ar(f),ar(g) > 0 und ar(a) =ar(b) = 0
• typische Relationsnamen: R,S,...

Definition

Die Menge der Variablen ist Var=\{x_0,x_1 ,...\}.

Definition

Sei \sum eine Signatur. Die Menge T_{\sum} der $\sum$-Terme ist induktiv definiert:

1. Jede Variable ist ein Term, d.h. Var\subseteq T_{\sum}
2. ist f\in\Omega mit ar(f)=k und sind t_1,...,t_k\in T_{\sum}, so gilt f(t_1,...,t_k)\in T_{\sum}
3. Nichts ist $\sum$-Term, was sich nicht mittels der obigen Regeln erzeugen läßt.

Beispiel:In der Signatur der Datenbank von vorhin haben wir u.a. die folgenden Terme:

• x_1 und x_8
• f(x_0) und f(f(x_3))
• dk() und f(dk()) - hierfür schreiben wir kürzer dk bzw. f(dk)

Definition

Sei \sum Signatur. Die atomaren $\sum$-Formeln sind die Zeichenketten der Form

• R(t_1,t_2,...,t_k) falls t_1,t_2,...,t_k\in T_{\sum} und R\in Rel mit ar(R)=k oder
• t_1=t_2 falls t_1,t_2\in T_{\sum} oder
• \bot.

Beispiel: In der Signatur der Datenbank von vorhin haben wir u.a. die folgenden atomaren Formeln:

• S(x_1) und LuLP(f(x4))
• S(dk) und AuD(f(dk))

Definition

Sei \sum Signatur. $\sum$-Formeln werden durch folgenden induktiven Prozeß definiert:

1. Alle atomaren $\sum$-Formeln sind $\sum$-Formeln.
2. Falls \varphi und \Psi $\sum$-Formeln sind, sind auch (\varphi\wedge\Psi),$(\varphi\vee\Psi)$ und (\varphi\rightarrow\Psi) $\sum$-Formeln.
3. Falls \varphi eine $\sum$-Formel ist, ist auch \lnot\varphi eine $\sum$-Formel.
4. Falls \varphi eine $\sum$-Formel und x\in Var, so sind auch \forall x\varphi und \exists x\varphi $\sum$-Formeln.
5. Nichts ist $\sum$-Formel, was sich nicht mittels der obigen Regeln erzeugen läßt.

Ist die Signatur \sum aus dem Kontext klar, so sprechen wir einfach von Termen, atomaren Formeln bzw.Formeln.

Beispiel:In der Signatur der Datenbank von vorhin haben wir u.a. die folgenden Formeln:

• \forall x_0 (S(x_0)\vee WM(x_0)\vee Pr(x_0))
• Pr(dk)
• \forall x_3 (S(x_3)\rightarrow\lnot Pr(x_3))
• \forall x_0 \forall x_2 ((S(x_0)\wedge Pr(x_2))\rightarrow J(x_0,x_2))
• \exists x_1 (LuLP(x_1)\wedge AuD(x_1))
• \exists x_2 ((\lnot LuLP(x_2)\vee\lnot AuD(x_2))\wedge\lnot WM(x_2))
• \forall x_1 (S(x_1)\rightarrow J(x_1,f(x_1)))

Wir verwenden die aus der Aussagenlogik bekannten Abkürzungen, z.B. steht \varphi\leftrightarrow\Psi für (\varphi\rightarrow\Psi)\wedge(\Psi\rightarrow\varphi).

Zur verbesserten Lesbarkeit fügen wir mitunter hinter quantifizierten Variablen einen Doppelpunkt ein, z.B. steht \exists x\forall y:\varphi für \exists x\forall y\varphi

Ebenso verwenden wir Variablennamen x,$y$,$z$ u.ä.

Präzedenzen: \lnot,\forall x,\exists x binden am stärksten

Beispiel: (\lnot\forall x:R(x,y)\wedge\exists z:R(x,z))\rightarrow P(x,y,z) steht für ((\lnot(\forall x:R(x,y))\wedge\exists z:R(x,z))\rightarrow P(x,y,z))

Aufgabe

Im folgenden seien

• P ein-stelliges, Q und R zwei-stellige Relationssymbole,
• a null-stelliges und f ein-stelliges Funktionssymbol und
• x,y und z Variable.

Welche der folgenden Zeichenketten sind Formeln?

\forall x P(a)	ja
\forall x\exists y(Q(x,y)\vee R(x))	nein
\forall x Q(x,x)\rightarrow\exists x Q(x,y)	ja
\forall x P(f(x))\vee\forall x Q(x,x)$	ja
\forall x(P(y)\wedge\forall y P(x))	ja
P(x) \rightarrow\exists x Q(x,P(x))	nein
\forall f\exists x P(f(x))	nein

Definition

Sei \sum eine Signatur. Die Menge FV(\varphi) der freien Variablen einer $\sum$-Formel \varphi ist induktiv definiert:

• Ist \varphi atomare $\sum$-Formel, so ist FV(\varphi) die Menge der in \varphi vorkommenden Variablen.
• FV(\varphi\Box\Psi) =FV(\varphi)\cup FV(\Psi) für \Box\in\{\wedge,\vee,\rightarrow\}
• FV(\lnot\varphi) =FV(\varphi)
• FV(\exists x\varphi) =FV(\forall x\varphi) =FV(\varphi)\backslash\{x\}. Eine $\sum$-Formel \varphi ist geschlossen oder ein $\sum$-Satz, wenn FV(\varphi)=\varnothing gilt.

Was sind die freien Variablen der folgenden Formeln? Welche Formeln sind Sätze?

	freie Variablen?	Satz?
\forall x P(a)	nein	ja
\forall x Q(x,x)\rightarrow\exists x Q(x,y)	y	nein
\forall x P(x)\vee\forall x Q(x,x)	nein	ja
\forall x(P(y)\wedge\forall y P(x))	y	nein
\forall x(\lnot\forall y Q(x,y)\wedge R(x,y))	y	nein
\exists z(Q(z,x)\vee R(y,z))\rightarrow\exists y(R(x,y)\wedge Q(x,z))	x,y,z	nein
\exists x(\lnot P(x)\vee P(f(a)))	nein	ja
P(x)\rightarrow\exists x P(x)	x	nein
\exists x\forall y((P(y)\rightarrow Q(x,y))\vee\lnot P(x))	x	nein
\exists x\forall x Q(x,x)	nein	ja

Semantik der Prädikatenlogik

• Erinnerung: Die Frage „Ist die aussagenlogische Formel \varphi wahr oder falsch?“ war sinnlos, denn wir wissen i.a. nicht, ob die atomaren Aussagen wahr oder falsch sind.
• Analog: Die Frage „Ist die prädikatenlogische Formel \varphi wahr oder falsch?“ ist sinnlos, denn wir wissen bisher nicht, über welche Objekte, über welche „Struktur“ \varphi spricht.

Definition

Sei \sum eine Signatur. Eine $\sum$-Struktur ist ein Tupel A=(U_A,(f^A)_{f\in\Omega},(R^A)_{R\in Rel}), wobei

• U_A eine nichtleere Menge, das Universum,
• R^A\supseteq U_A^{ar(R)} eine Relation der Stelligkeit ar(R) für R\in Rel und
• f^A:U_A^{ar(f)}\rightarrow U_A eine Funktion der Stelligkeit ar(f) für f\in\Omega ist.

Bemerkung: U_A^0=\{()\}.

• Also ist a^A:U_A^0\rightarrow U_A für a\in\Omega mit ar(a)=0 vollständig gegeben durch a^A(())\in U_A. Wir behandeln 0-stellige Funktionen daher als Konstanten.
• Weiterhin gilt R^A=\varnothing oder R^A=\{()\} für R\in Rel mit ar(R)=0.

Beispiel: Graph

• Sei \sum=(\Omega ,Rel,ar) mit \Omega=\varnothing ,Rel=\{E\} und ar(E)=2 die Signatur der Graphen.
• Um den Graphen als $\sum$-Struktur A=(UA,EA) zu betrachten, setzen wir
  • UA=\{v_1,v_2,...,v_9\} und
  • EA=\{(v_i,v_j)|(v_i,v_j) ist Kante\}

Im folgenden sei \sum eine Signatur, A eine $\sum$-Struktur und \rho:Var\rightarrow U_A eine Abbildung (eine Variableninterpretation). Wir definieren eine Abbildung \rho′:T\sum\rightarrow U_A induktiv für t\in T_{\sum}:

• ist t\in Var, so setze \rho′(t) =\rho(t)
• ansonsten existieren f\in\Omega mit ar(f)=k und t_1,...,t_k\in T_{\sum} mit t=f(t_1,...,t_k). Dann setze \rho′(t) =f^A(\rho′(t_1),...,\rho′(t_k)). Die Abbildung \rho′ ist die übliche „Auswertungsabbildung“. Zur Vereinfachung schreiben wir auch \rho(t) an Stelle von \rho′(t).

Beispiel:

• Seien A=(R,f^A,a^A) mit f^A die Subtraktion und a nullstelliges Funktionssymbol mit a^A=10. Seien weiter x,y\in Var mit \rho(x)=7 und \rho(y)=-2. Dann gilt \rho(f(a,f(x,y))) =\rho(a)-(\rho(x)-\rho(y)) =a^A-(\rho(x)-\rho(y)) = 1
• Seien A= (Z,f^A,a^A) mit f^A die Maximumbildung, a nullstelliges Funktionssymbol mit a^A=10. Seien weiter x,y\in Var mit \rho(x)=7 und \rho(y)=-2. In diesem Fall gilt \rho(f(a,f(x,y))) = max(\rho(a),max(\rho(x),\rho(y)) = max(a^A,max(\rho(x),\rho(y))) = 10

Bemerkung: Wir müssten also eigentlich noch vermerken, in welcher Struktur \rho(t) gebildet wird – dies wird aber aus dem Kontext immer klar sein.

Für eine $\sum$-Formel \varphi definieren wir die Gültigkeit in einer $\sum$-Struktur A unter der Variableninterpretation \rho (in Zeichen: A\Vdash_\rho\varphi) induktiv:

• A\Vdash_\rho\bot gilt nicht.
• A\Vdash_\rho R(t_1,...,t_k) falls (\rho(t_1),...,\rho(t_k))\in R^A für R\in Rel mit ar(R)=k und t_1,...,t_k\in T_{\sum}.
• A\Vdash_\rho t_1 =t_2 falls \rho(t_1) =\rho(t_2) für t_1,t_2\in T_{\sum}.

Für $\sum$-Formeln \varphi und \Psi und x\in Var:

• A\Vdash_p \varphi\wedge\Psi falls A\Vdash_p\varphi und A\Vdash_p \Psi.
• A\Vdash_p \varphi\vee\Psi falls A\Vdash_p\varphi oder A\Vdash_p\Psi .
• A\Vdash_p \varphi\rightarrow\Psi falls nicht A\Vdash_p\varphi oder A\Vdash_p\Psi .
• A\Vdash_p \lnot\varphi falls A\Vdash_p \varphi nicht gilt.
• A\Vdash_p \exists x\varphi falls ???
• A\Vdash_p \forall x\varphi falls ???

Für x\in Var und a\in U_A sei \rho[x\rightarrow a]:Var\rightarrow U_A die Variableninterpretation, für die gilt (\rho[x\rightarrow a])(y) = \begin{cases} \rho(y) \quad\text{ falls } x\not=y \\ a \quad\text{ sonst } \end{cases}

• A\Vdash_p \exists x\varphi falls es a\in U_A gibt mit A\Vdash_{p[x\rightarrow a]}\varphi.
• A\Vdash_p \forall x\varphi falls A\Vdash_{p[x\rightarrow a]}\varphi für alle a\in U_A.

Definition

Sei \sum eine Signatur, \varphi eine $\sum$-Formel, \Delta eine Menge von $\sum$-Formeln und A eine $\sum$-Struktur.

• A\Vdash\varphi (A ist Modell von \varphi) falls A\Vdash_p\varphi für alle Variableninterpretationen \rho gilt.
• A\Vdash\Delta falls A\Vdash\Psi für alle \Psi\in\Delta.

Aufgaben

• Sei A die Struktur, die dem vorherigen Graphen entspricht
• Welche der folgenden Formeln \varphi gelten in A, d.h. für welche Formeln gilt A\Vdash_p\varphi für alle Variableninterpretationen \rho?
  1. \exists x\exists y:E(x,y)
  2. \forall x\exists y:E(x,y)
  3. \exists x\forall y:(x\not=y\rightarrow E(x,y))
  4. \forall x\forall y:(x\not=y\rightarrow E(x,y))
  5. \exists x\exists y\exists z:(E(x,y)\wedge E(y,z)\wedge E(z,x))
• In der Prädikatenlogik ist es also möglich, die Eigenschaften vom Anfang des Kapitels auszudrücken, ohne den Graphen direkt in die Formel zu kodieren.

Definition

Sei \sum eine Signatur, \varphi eine $\sum$-Formel, \Delta eine Menge von $\sum$-Formeln und A eine $\sum$-Struktur.

• \Delta ist erfüllbar, wenn es $\sum$-Struktur B und Variableninterpretation \rho:Var\rightarrow U_B gibt mit B\Vdash_\rho\Psi für alle \Psi\in\Delta.
• \varphi ist semantische Folgerung von \Delta(\Delta\Vdash\varphi) falls für alle $\sum$-Strukturen B und alle Variableninterpretationen \rho:Var\rightarrow U_B gilt: Gilt B\Vdash_\rho\Psi für alle \Psi\in\Delta, so gilt auch B\Vdash_\rho \varphi.
• \varphi ist allgemeingültig, falls B\Vdash \rho\varphi für alle $\sum$-Strukturen B und alle Variableninterpretationen \rho gilt.

Bemerkung: \varphi allgemeingültig gdw. \varnothing\Vdash\varphi gdw. \{\lnot\varphi\} nicht erfüllbar. Hierfür schreiben wir auch \Vdash\varphi.

Beispiel: Der Satz \varphi=(\forall x:R(x)\rightarrow\forall x:R(f(x))) ist allgemeingültig.

Beweis: Sei \sum Signatur, so dass \varphi $\sum$-Satz ist. Sei A $\sum$-Struktur und \rho Variableninterpretation. Wir betrachten zwei Fälle:

1. Falls A\not\Vdash_\rho\forall x R(x), so gilt A\Vdash_p\varphi.
2. Wir nehmen nun A\Vdash_p\forall x R(x) an. Sei a\in U_A beliebig und b=f^A(a). A\Vdash_p\forall x R(x) \Rightarrow A\Vdash_{p[x\rightarrow b]} R(x) \Rightarrow RA\owns (p[x\rightarrow b])(x) = b = f^A(a) = (\rho[x\rightarrow a])(f(x)) \Rightarrow A\Vdash_{p[x\rightarrow a]}R(f(x)). Da a\in U_A beliebig war, haben wir also A\Vdash_p\forall x:R(f(x)). Also gilt auch in diesem Fall A\Vdash_p\varphi. Da A und \rho beliebig waren, ist \varphi somit allgemeingültig.

Beispiel:

• Der Satz \varphi =\exists x(R(x)\rightarrow R(f(x))) ist allgemeingültig.
• Beweis: Sei \sum Signatur, so dass \varphi $\sum$-Satz ist. Sei A $\sum$-Struktur und \rho Variableninterpretation. Wir betrachten wieder zwei Fälle:
  1. Angenommen, R^A=U_A. Sei a\in U_A beliebig.
     • \Rightarrow f^A(a)\in R^A
     • \Rightarrow A\Vdash_{p[x\rightarrow a]} R(f(x))
     • \Rightarrow A\Vdash_{p[x\rightarrow a]} R(x)\rightarrow R(f(x))
     • \Rightarrow A\Vdash_p\varphi.
  2. Ansonsten existiert a\in U_A\backslash R^A.
     • \Rightarrow A\not\Vdash_{p[x\rightarrow a]} R(x)
     • \Rightarrow A\Vdash_{p[x\rightarrow a]} R(x)\rightarrow R(f(x))
     • \Rightarrow A\Vdash_p \varphi. Da A und \rho beliebig waren, ist \varphi somit allgemeingültig.

Aufgabe

	allgemeingültig	erfüllbar	unerfüllbar
P(a)	nein	ja	nein
\exists x:(\lnot P(x)\vee P(a))	ja	ja	nein
P(a)\rightarrow\exists x:P(x)	ja	ja	nein
P(x)\rightarrow\exists x:P(x)	ja	ja	nein
\forall x:P(x)\rightarrow\exists x:P(x)	ja	ja	nein
\forall x:P(x)\wedge\lnot\forall y:P(y)	nein	nein	ja
\forall x:(P(x,x)\rightarrow\exists x\forall y:P(x,y))	nein	ja	nein
\forall x\forall y:(x=y\rightarrow f(x) =f(y))	ja	ja	nein
\forall x\forall y:(f(x) =f(y)\rightarrow x=y)	nein	ja	nein
\exists x\exists y\exists z:(f(x) =y\wedge f(x) =z\wedge y \not=z)	nein	nein	ja
\exists x\forall x:Q(x,x)	nein	ja	nein

Substitutionen

Definition

Eine Substitution besteht aus einer Variable x\in Var und einem Term t\in T_{\sum}, geschrieben [x:=t].

Die Formel \varphi[x:=t] ist die Anwendung der Substitution [x:=t] auf die Formel \varphi. Sie entsteht aus \varphi, indem alle freien Vorkommen von x durch t ersetzt werden. Sie soll das über t aussagen, was \varphi über x ausgesagt hat. Dazu definieren wir zunächst induktiv, was es heißt, die freien Vorkommen von x im Term s\in T_{\sum} zu ersetzen:

• x[x:=t] =t
• y[x:=t] =y für y\in Var\backslash\{x\}
• (f(t_1 ,...,t_k))[x:=t] =f(t_1 [x:=t],...t_k[x:=t]) für f\in\Omega mit ar(f) =k und t_1,...,t_k\in T_{\sum}

Lemma

Seien \sum Signatur, A $\sum$-Struktur, \rho:Var\rightarrow U_A Variableninterpretation, x\in Var und s,t\in T_{\sum}. Dann gilt \rho(s[x:=t])=\rho[x\rightarrow \rho(t)](s).

Beweis: Induktion über den Aufbau des Terms s (mit \rho′=\rho[x\rightarrow \rho(t)] ):

• s=x:\rho(s[x:=t])=\rho(t) =\rho′(x) =\rho′(s)
• s\in Var\backslash\{x\}:\rho(s[x:=t])=\rho(s) =\rho′(s)
• s=f(t_1 ,...,t_k):\rho((f(t_1 ,...,t_k))[x:=t])= \rho(f(t_1[x:=t],...,t_k[x:=t]))= f^A(\rho(t_1[x:=t]),...,\rho(t_k[x:=t])) = f^A(\rho′(t_1),...,\rho′(t_k))= \rho′(f(t_1 ,...,t_k))=\rho′(s)

Die Definition von s[x:=t] kann induktiv auf $\sum$-Formeln fortgesetzt werden:

• (t_1 =t_2 )[x:=t] = (t_1 [x:=t] =t_2 [x:=t]) für t_1 ,t_2 \in T_{\sum}
• (R(t_1 ,...,t_k))[x:=t] =R(t_1 [x:=t],...,t_k[x:=t]) für R\in Rel mit ar(R) =k und t_1 ,...,t_k\in T_{\sum}
• \bot[x:=t] =\bot

Für \sum -Formeln \varphi und \Psi und y\in Var:

• (\varphi\Box\Psi)[x:=t]=\varphi [x:=t]\Box\Psi[x:=t] für \Box\in\{\wedge,\vee,\rightarrow\}
• (\lnot\varphi)[x:=t] = \lnot(\varphi[x:=t])
• (Qy\varphi)[x:=t] = \begin{cases} Qy\varphi[x:=t] \quad\text{ falls } x\not=y \\ Qy\varphi \quad\text{ falls } x=y \end{cases} \text{ für } Q\in\{\exists,\forall\}.

Beispiel: (\exists x P(x,f(y))\vee\lnot\forall yQ(y,g(a,h(z))))[y:=f(u)] = (\exists x P(x,f(f(u)))\vee\lnot\forall yQ(y,g(a,h(z))))

\varphi [x:=t] „soll das über t aussagen, was \varphi über x ausgesagt hat.“

Gegenbeispiel: Aus \exists y Mutter(x) =y mit Substitution [x:=Mutter(y)] wird \exists y Mutter$(Mutter(y)) =y$.

Definition

Sei [x:=t] Substitution und \varphi $\sum$-Formel. Die Substitution [x:=t] heißt für \varphi zulässig, wenn für alle y\in Var gilt: y Variable in t\Rightarrow\varphi enthält weder \exists y noch \forall y

Lemma

Sei \sum Signatur, A $\sum$-Struktur, \rho:Var\rightarrow U_A Variableninterpretation, x\in Var und t\in T_{\sum}. Ist die Substitution [x:=t] für die $\sum$-Formel \varphi zulässig, so gilt A\Vdash_p\varphi [x:=t]\Leftrightarrow A\Vdash_{p[x\rightarrow \rho(t)]}\varphi.

Beweis: Induktion über den Aufbau der Formel \varphi (mit \rho'=\rho[x\rightarrow \rho(t)]):

• \varphi = (s_1 =s_2):
  • A\Vdash_p(s_1 =s_2)[x:=t] \Leftrightarrow A\Vdash_p s_1[x:=t] =s_2[x:=t]
  • \Leftrightarrow \rho(s_1[x:=t]) =\rho(s_2[x:=t])\Leftrightarrow \rho'(s_1) =\rho'(s_2)
  • \Leftrightarrow A\Vdash_{p′} s_1 =s_2
  • andere atomare Formeln analog
• \varphi =\varphi_1\wedge\varphi_2:
  • A\Vdash_p(\varphi_1\wedge\varphi_2)[x:=t] \Leftrightarrow A\Vdash_p\varphi_1 [x:=t]\wedge\varphi_2[x:=t]
  • \Leftrightarrow A\Vdash_p\varphi_1[x:=t] und A\Vdash_p\varphi_2[x:=t]
  • \Leftrightarrow A\Vdash_{p′}\varphi_1 und A\Vdash_{p′}\varphi_2
  • \Leftrightarrow A\Vdash_{p′}\varphi_1\wedge\varphi_2
  • \varphi=\varphi_1\vee\varphi_2,\varphi =\varphi_1\rightarrow\varphi_2 und \varphi=\lnot\psi analog
• \varphi=\forall y\psi:
  • Wir betrachten zunächst den Fall x=y:
    • A\Vdash_p(\forall x\psi)[x:=t]\Leftrightarrow A\Vdash_p\forall x\psi \Leftrightarrow A\Vdash_{p′}\forall x\psi (denn x\not\in FV(\forall x\psi) )
  • Jetzt der Fall x\not=y:
    • Für a\in U_A setze \rho_a=\rho[y\rightarrow a]. Da [x:=t] für \varphi zulässig ist, kommt y in t nicht vor. Zunächst erhalten wir
    • \rho_a[x\rightarrow \rho_a(t)] = \rho_a[x\rightarrow \rho(t)] da y nicht in t vorkommt
    • =\rho[y\rightarrow a][x\rightarrow \rho(t)] = \rho[x\rightarrow \rho(t)][y\rightarrow a] da x\not=y
    • Es ergibt sich A\Vdash_p(\forall y\psi)[x:=t]\Leftrightarrow A\Vdash_p\forall y(\psi[x:=t]) (wegen x\not=y)
    • \Leftrightarrow A\Vdash_{pa}\psi[x:=t] für alle a\in U_A
    • \Leftrightarrow A\Vdash_{pa[x\rightarrow \rho_a(t)]}\psi für alle a\in U_A
    • \Leftrightarrow A\Vdash_{p[x\rightarrow \rho(t)][y\rightarrow a]}\psi für alle a\in U_A
    • \Leftrightarrow A\Vdash_{p[x\rightarrow \rho(t)]}\forall y\psi
• \varphi=\exists y\psi : analog

Natürliches Schließen

Wir haben Regeln des natürlichen Schließens für aussagenlogische Formeln untersucht und für gut befunden. Man kann sie natürlich auch für prädikatenlogische Formeln anwenden.

Beispiel: Für alle $\sum$-Formel \varphi und \psi gibt es eine Deduktion mit Hypothesen in \{\lnot\varphi\wedge\lnot\psi\} und Konklusion \lnot(\varphi\vee\psi):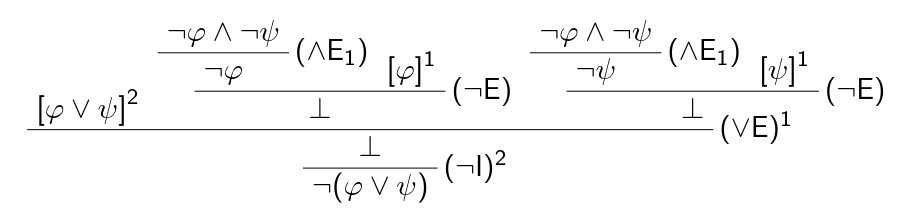

Korrektheit

Können wir durch mathematische Beweise zu falschen Aussagen kommen? Können wir durch das natürliche Schließen zu falschen Aussagen kommen? Existiert eine Menge \Gamma von $\sum$-Formeln und eine $\sum$-Formel \varphi mit \Gamma\vdash\varphi und \Gamma\not\Vdash\varphi?

Frage: Gilt \Gamma\vdash\varphi\Rightarrow \Gamma\Vdash\varphi bzw. \varphi ist Theorem \Rightarrow\varphi ist allgemeingültig?

Der Beweis des Korrektheitslemmas für das natürliche Schließen kann ohne große Schwierigkeiten erweitert werden. Man erhält

Lemma V0

Sei \sum eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik verwendet. Dann gilt \Gamma\Vdash\varphi.

Umgekehrt ist nicht zu erwarten, dass aus \Gamma\Vdash\varphi folgt, dass es eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi gibt, denn die bisher untersuchten Regeln erlauben keine Behandlung von =,\forall bzw. \exists. Solche Regeln werden wir jetzt einführen.

Zunächst kümmern wir uns um Atomformeln der Form t_1 =t_2. Hierfür gibt es die zwei Regeln (R) und (GfG):

Reflexivität (ausführlich)

Für jeden Termt ist \frac{}{t=t} eine hypothesenlose Deduktion mit Konklusion t=t.

Gleiches-für-Gleiches in mathematischen Beweisen

,,Zunächst zeige ich, dass s die Eigenschaft \varphi hat:... Jetzt zeige ich s=t:... Also haben wir gezeigt, dass t die Eigenschaft \varphi hat. qed''

Gleiches-für-Gleiches (ausführlich) Seien s und t Terme und \varphi Formel, so dass die Substitutionen [x:=s] und [x:=t] für \varphi zulässig sind. Sind D und E Deduktionen mit Hypothesen in \Gamma und Konklusionen \varphi[x:=s] bzw. s=t, so ist das folgende eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi[x:=t]:

Gleiches-für-Gleiches (Kurzform) Bedingung: über keine Variable aus s oder t wird in \varphi quantifiziert

Die folgenden Beispiele zeigen, dass wir bereits jetzt die üblichen Eigenschaften der Gleichheit (Symmetrie, Transitivität, Einsetzen) folgern können.

Beispiel: Seien x Variable, s Term ohne x und \varphi=(x=s).

• Da \varphi quantorenfrei ist, sind die Substitutionen [x:=s] und [x:=t] für \varphi zulässig.
• Außerdem gelten \varphi[x:=s] = (s=s) und \varphi[x:=t] = (t=s).
• Also ist das folgende eine Deduktion:
• Für alle Termesundthaben wir also \{s=t\}\vdash t=s.

Beispiel: Seien x Variable, r,s und t Terme ohne x und \varphi=(r=x).

• Da \varphi quantorenfrei ist, sind die Substitutionen [x:=s] und [x:=t] für \varphi zulässig.
• Außerdem gelten \varphi[x:=s]=(r=s) und \varphi[x:=t]=(r=t).
• Also ist das folgende eine Deduktion:
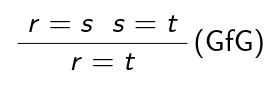
• Für alle Terme r,s und t haben wir also \{r=s,s=t\}\vdash r=t.

Beispiel: Seien x Variable, s und t Terme ohne x,$f$ einstelliges Funktionssymbol und \varphi=(f(s)=f(x)).

• Da \varphi quatorenfrei ist, sind die Substitutionen [x:=s] und [x:=t] für \varphi zulässig.
• Außerdem gelten \varphi[x:=s]=(f(s)=f(s)) und \varphi[x:=t]=(f(s)=f(t)).
• Also ist das folgende eine Deduktion:

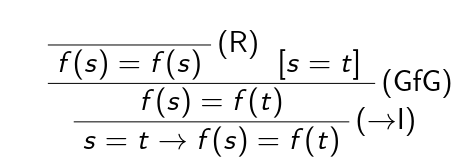
Lemma V1

Sei \sum eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik, (R) und (GfG) verwendet. Dann gilt \Gamma\Vdash\varphi.

Beweis: Wir erweitern den Beweis des Korrektheitslemmas bzw. des Lemmas V0, der Induktion über die Größe der Deduktion D verwendete.

• Wir betrachten nur den Fall, dass D die folgende Form hat:
• Da dies Deduktion ist, sind die Substitutionen [x:=s] und [x:=t] für \varphi zulässig, d.h. in \varphi wird über keine Variable aus s oder t quantifiziert.
• E und F kleinere Deduktionen \Rightarrow\Gamma\Vdash\varphi[x:=s] und \Gamma\Vdash s=t
• Seien A $\sum$-Struktur und \rho Variableninterpretation mit A\Vdash_p\gamma für alle \gamma\in\Gamma.
  • \Rightarrow A\Vdash_p\varphi[x:=s] und A\Vdash_p s=t
  • \Rightarrow A\Vdash_{p[x\rightarrow \rho(s)]}\varphi und \rho(s) =\rho(t)
  • \Rightarrow A\Vdash_{p[x\rightarrow \rho(t)]}\varphi
  • \Rightarrow A\Vdash_p \varphi[x:=t]
• Da A und \rho beliebig waren mit A\Vdash_p\gamma für alle \gamma\in\Gamma haben wir \Gamma\Vdash\varphi[x:=t] gezeigt.

\forall in math. Beweisen

Ein mathematischer Beweis einer Aussage „für alle x gilt $\varphi$“ sieht üblicherweise so aus: "Sei x beliebig, aber fest. Jetzt zeige ich \varphi (hier steckt die eigentliche Arbeit). Da x beliebig war, haben wird „für alle x gilt $\varphi$“ gezeigt. qed“

\forall -Einführung

Sei D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi und sei x eine Variable, die in keiner Formel aus \Gamma frei vorkommt. Dann ist das folgende eine Deduktion mit Hypothesen in \Gamma und Konklusion \forall x\varphi: \frac{\phi}{\forall x\varphi}

Bedingung: x kommt in keiner Hypothese frei vor

Lemma V2

Sei \sum eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik, (R), (GfG) und (\forall -I) verwendet. Dann gilt \Gamma\Vdash\varphi.

Beweis: Betrachte die folgende Deduktion D

• Insbesondere ist x keine freie Variable einer Formel aus \Gamma und es gilt nach IV \Gamma\Vdash\varphi
• Sei nun A $\sum$-Struktur und \rho Variableninterpretation mit A\Vdash_p y für alle y\in\Gamma.
• Zu zeigen ist A\Vdash_p \forall x\varphi:
  • Sei also a\in U_A beliebig.
  • \Rightarrow für alle y\in\Gamma gilt A\Vdash_{p[x\rightarrow a]} y da x\not\in FV(y) und A\Vdash_p y
  • \Rightarrow A\Vdash_{\rho[x\rightarrow a]}\varphi
  • Da a\in U_A beliebig war, haben wir A\Vdash_\rho\forall x\varphi gezeigt
• Da A und \rho beliebig waren mit A\Vdash_\rho\Gamma für alle \gamma\in\Gamma haben wir also \Gamma\Vdash\forall x\varphi gezeigt.

\forall -Elimination in math. Beweisen

Ein mathematischer Beweis einer Aussage „t erfüllt $\varphi$“ kann so aussehen: „Zunächst zeige ich \forall x\varphi (hier steckt die eigentliche Arbeit). Damit erfüllt insbesondere t die Aussage$\varphi$ , d.h., wir haben „t erfüllt $\varphi$“ gezeigt. qed“

\forall -Elimination

Sei D eine Deduktion mit Hypothesen in \Gamma und Konklusion \forall x\varphi und seit Term, so dass Substitution [x:=t] für \varphi zulässig ist. Dann ist das folgende eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi[x:=t]:\frac{\forall x\varphi}{\varphi[x:=t]}

Bedingung: über keine Variable aus t wird in \varphi quantifiziert

Lemma V3

Sei \sum eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik, (R), (GfG), ($\forall$-I) und ($\forall$-E) verwendet. > Dann gilt \Gamma\Vdash\varphi.

Beweis: Analog zum Beweis von Lemma V2.

\exists in math. Beweisen

Ein Beweis von „\sigma gilt“ kann so aussehen: „Zunächst zeige ich \exists x\varphi (hier steckt Arbeit). Jetzt zeige ich, dass \sigma immer gilt, wenn$\varphi$ gilt (mehr Arbeit). Damit gilt \sigma. qed“

\exists -Elimination

Sei \Gamma eine Menge von Formeln, die die Variable x nicht frei enthalten und enthalte die Formel \sigma die Variabel x nicht frei. Wenn D eine Deduktion mit Hypothesen in \Gamma und Konklusion \exists x\varphi und E eine Deduktion mit Hypothesen in $\Gamma $\cup${\varphi}$ und Konklusion \sigma ist, dann ist das folgende eine Deduktion mit Hypothesen in \Gamma und Konklusion \sigma:\frac{\exists x\varphi \quad\quad \sigma}{\sigma}

Bedingung: x kommt in den Hypothesen und in \sigma nicht frei vor

Lemma V4 Sei \sigma eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine \sigma -Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik, (R), (GfG), ($\forall$-I), ($\forall$-E) und ($\exists$-E) verwendet. Dann gilt \Gamma\Vdash\varphi.

Beweis: Sei D die folgende Deduktion

• Insbesondere kommt x in den Formeln aus \Gamma\cup\{\sigma\} nicht frei vor. Außerdem gelten nach IV \Gamma\Vdash\exists x\varphi und \Gamma\cup\{\varphi\}\Vdash\sigma.
• Sei nun A $\sigma$-Struktur und \rho Variableninterpretation mit A\Vdash_\rho\Gamma für alle \gamma\in\Gamma.
• Zu zeigen ist A\Vdash_\rho\sigma:
  • Wegen A\Vdash_\rho\exists x\varphi existiert a\in U_A mit A\Vdash_{\rho[x\rightarrow a]}\varphi.
  • x kommt in Formeln aus \Gamma nicht frei vor \Rightarrow A\Vdash_{\rho[x\rightarrow a]}\gamma für alle \gamma\in\Gamma.
  • Aus \Gamma\cup\{\varphi\}\Vdash\sigma folgt A\Vdash_{\rho[x\rightarrow a]}\sigma.
  • Da x\not\in FV(\sigma) erhalten wir A\Vdash_\rho \sigma.
• Da A und \rho beliebig waren mit A\Vdash_\rho\gamma für alle \gamma\in\Gamma haben wir also \Gamma\Vdash\sigma gezeigt.

\exists -Einführung in math. Beweisen

Ein mathematischer Beweis einer Aussage „es gibt ein x, das \varphi erfüllt“ sieht üblicherweise so aus: „betrachte dieses t (hier ist Kreativität gefragt). Jetzt zeige ich, daß t\varphi erfüllt (u.U. harte Arbeit). Also haben wir „es gibt ein x, das \varphi erfüllt“ gezeigt. qed“

\exists -Einführung

Sei die Substitution [x:=t] für die Formel \varphi zulässig. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi[x:=t]. Dann ist das folgende eine Deduktion mit Hypothesen in \Gamma und Konklusion \exists x\varphi:\frac{\varphi[x:=t]}{\exists x\varphi}

Bedingung: über keine Variable in t wird in \varphi quantifiziert

Korrektheitslemma für das natürliche Schließen in der Prädikatenlogik

Sei \sigma eine Signatur, \Gamma eine Menge von $\sum$-Formeln und \varphi eine \sigma -Formel. Sei weiter D eine Deduktion mit Hypothesen in \Gamma und Konklusion \varphi, die die Regeln des natürlichen Schließens der Aussagenlogik, (R), (GfG), ($\forall$-I), ($\forall$-E), (\exists -E) und (\exists -I) verwendet. Dann gilt \Gamma\Vdash\varphi.

Beweis: analog zu obigen Beweisen.

Regeln des natürlichen Schließens (Erweiterung)

• (R): \frac{}{t=t}
• (GfG): \frac{\varphi[x:=s] \quad\quad s=t}{\varphi[x:=t]} (über keine Variable aus s oder t wird in \varphi quantifiziert)
• ($\forall$-I): \frac{\varphi}{\forall x\varphi} (x nicht frei in Hypothesen)
• ($\forall$-E): \frac{\forall x\varphi}{\varphi[x:=t]} (über keine Variable aus t wird in \varphi quantifiziert)
• ($\exists$-I): \frac{\varphi [x:=t]}{\exists x\varphi} (über keine Variable aus t wird in \varphi quantifiziert)
• ($\exists$-I): \frac{\exists x\varphi\quad\quad \sigma}{\sigma} (x kommt in Hypothesen und \sigma nicht frei vor)

Definition

Für eine Menge \Gamma von $\sum$-Formeln und eine $\sum$-Formel \varphi schreiben wir \Gamma\vdash\varphi wenn es eine Deduktion gibt mit Hypothesen in \Gamma und Konklusion \varphi. Wir sagen „\varphi ist eine syntaktische Folgerung von $\Gamma$“. Eine Formel \varphi ist ein Theorem, wenn \varnothing\vdash\varphi gilt.

Bemerkung: \Gamma\vdash\varphi sagt (zunächst) nichts über den Inhalt der Formeln in \Gamma\cup\{\varphi\} aus, sondern nur über den Fakt, dass \varphi mithilfe des natürlichen Schließens aus den Formeln aus \Gamma hergeleitet werden kann. Ebenso sagt „\varphi ist Theorem“ nur, dass \varphi abgeleitet werden kann, über „Wahrheit“ sagt dieser Begriff (zunächst) nichts aus. Wir haben aber "en passant" das folgende gezeigt:

Korrektheitssatz

Für eine Menge von $\sum$-Formeln \Gamma und eine $\sum$-Formel \varphi gilt \Gamma\vdash\varphi \Rightarrow \Gamma\Vdash\varphi.

Beispiel: Seien \varphi Formel und x Variable. Dann gelten \{\lnot\exists x\varphi\}\Vdash\forall x\lnot\varphi und \{\forall x\lnot\varphi\}\Vdash\lnot\exists x\varphi.

• Beweis:

Beispiel: Seien \varphi Formel und x Variable. Dann gelten \{\lnot\forall x\varphi\}\Vdash \exists x\lnot\varphi und \{\exists x\lnot\varphi\}\Vdash\lnot\forall x\varphi.

• Beweis:

Vollständigkeit

Können wir durch mathematische Beweise zu allen korrekten Aussagen kommen? Können wir durch das natürliche Schließen zu allen korrekten Aussagen kommen?

Existiert eine Menge \Gamma von $\sum$-Formeln und eine $\sum$-Formel \varphi mit \Gamma\Vdash\varphi und \Gamma\not\vdash\varphi?

Frage: Gilt \Gamma\Vdash\varphi \Rightarrow \Gamma\vdash\varphi bzw. \varphi ist allgemeingültig \Rightarrow\varphi ist Theorem?

Plan:

• z.z. ist \Gamma\Vdash\varphi \Rightarrow \Gamma\vdash\varphi.
• dies ist äquivalent zu \Gamma\not\vdash\varphi \Rightarrow \Gamma\not\Vdash\varphi.
• hierzu geht man folgendermaßen vor:
  • \Gamma\not\vdash\varphi
  • \Leftrightarrow \Gamma\cup\{\lnot\varphi\} konsistent
  • \Rightarrow \exists\Delta\supseteq\Gamma\cup\{\lnot\varphi\} maximal konsistent
  • \Rightarrow \exists\Delta^+ \supseteq\Delta maximal konsistent mit Konkretisierung
  • \Rightarrow \Delta^+ erfüllbar
  • \Rightarrow \Delta erfüllbar
  • \Rightarrow \Gamma\cup\{\lnot\varphi\} erfüllbar
  • \Leftrightarrow \Gamma\cup\{\lnot\varphi\}

Definition

Eine Menge \Delta von Formeln hat Konkretisierungen, wenn für alle \exists x\varphi\in\Delta ein variablenloser Term t existiert mit \varphi[x:=t]\in\Delta.

Satz

Sei \Delta eine maximal konsistente Menge von $\sum$-Formeln. Dann existiert eine Signatur \sum^+ \supseteq\sum und eine maximal konsistente Menge von $\sum^+$-Formeln mit Konkretisierungen, so dass \Delta\subseteq\Delta^+.

Beweis: Wir konstruieren induktiv Signaturen \sum_n, maximal konsistente Menge von $\sum_n$-Formeln \Delta_n und konsistente Mengen von $\sum_{n+1}$-Formeln \Delta′_{n+1} mit

• \sum =\sum_0 \subseteq\sum_1 \subseteq\sum_2... und
• $\Delta = \Delta_0 \subseteq \Delta′_1 \subseteq\Delta_1 \subseteq\Delta′_2...$ und setzen dann
• \sum^+ =\bigcup_{n\geq 0} \sum_n und \Delta^+ = \bigcup_{n\geq 0} \Delta_n

1. IA: \sum_0 := \sum , \Delta_0:=\Delta
2. IV: Sei n\geq 0 und \Delta_n maximal konsistente Menge von $\sum_n$-Formeln. \psi=\exists x\varphi, ein „neues“ Konstantensymbol c_{\psi}
3. IS: \sum_{n+1}: alle Symbole aus \sum_n und, für jede Formel \psi\in\Delta_n der Form \Delta′_{n+1}:= \Delta_n\cup\{\varphi[x:=c_{\psi}]|\psi=\exists x\varphi\in\Delta_n\}
   • ohne Beweis: \Delta′_{n+1} ist konsistent
   • Idee: Ist \varphi $\sum_n$-Formel mit \Delta′_{n+1}\vdash\varphi, so gilt \Delta_n\vdash\varphi.
   • Konsistenz von \Delta′_{n+1} folgt mit \varphi=\bot
   • Analog zum Satz aus Vorlesung 4 existiert \Delta_{n+1}\supseteq \Delta'_{n+1} maximal konsistent

• Damit ist die Konstruktion der Signaturen \sum_n und der maximal konsistenten Mengen \Delta_n von $\sum_n$-Formeln abgeschlossen.
• noch z.z.: \Delta^+ hat Konkretisierungen und ist maximal konsistent
  • \Delta^+ hat Konkretisierungen: Sei \psi=\exists x\varphi\in\Delta^+
    • \Rightarrow es gibt n\geq 0 mit \psi\in\Delta_n
    • \Rightarrow \varphi[x:=c_{\psi}]\in\Delta′_{n+1}\subseteq \Delta_{n+1}\subseteq\Delta^+.
  • Konsistenz: (indirekt) angenommen, \Delta^+\vdash\bot
    • Da jede Deduktion endlich ist, existiert \Gamma\subseteq\Delta^+ endlich mit \Gamma\vdash\bot.
    • \Rightarrow es gibt n\geq 0 mit \Gamma\subseteq\Delta_n
    • \Rightarrow \Delta_n\vdash\bot - im Widerspruch zur Konsistenz von \Delta_n.
  • maximale Konsistenz: (indirekt) angenommen, \Delta^+ ist nicht maximal konsistent
    • \Rightarrow es gibt \Gamma\not\subseteq\Delta^+ konsistent
    • \Rightarrow es gibt \varphi\in\Gamma\backslash\Delta^+
    • \Rightarrow \Delta^+\cup\{\varphi\}\subseteq\Gamma konsistent
    • \varphi ist $\sum^+$-Formel \Rightarrow es gibt n\geq 0, so dass \varphi eine $\sum_n$-Formel ist.
    • \Delta_n maximal konsistente Menge von $\sum_n$-Formeln
    • \Rightarrow \varphi\in\Delta_n\subseteq\Delta^+ oder \lnot\varphi\in\Delta_n\subseteq\Delta^+
    • \Rightarrow \lnot\varphi\in\Delta^+\subseteq\Gamma
    • Also \varphi,\lnot\varphi\in\Gamma, im Widerspruch zur Konsistenz von \Gamma.

Satz

Sei \Delta^+ maximal konsistente Menge von $\sum^+$-Formeln mit Konkretisierungen. Dann ist \Delta^+ erfüllbar.

Beweisidee: Sei T die Menge der variablenlosen $\sum^+$-Terme. Auf T definieren wir eine Äquivalenzrelation ∼ durch $s∼t\Leftrightarrow \Delta^+\vdash(s=t)\Leftrightarrow (s=t)\in\Delta^+$ Sei A die folgende $\sum^+$-Struktur:

• U_A:=T/∼ ist die Menge der $∼$-Äquivalenzklassen
• R^A=\{([t_1],...,[t_k])|t_1 ,...,t_k\in T,R(t_1,...,t_k)\in\Delta^+\} für alle Relationssymbole R aus \sum^+
• f^A([t_1],...,[t_k]) = [f(t_1,...,t_k)] für alle t_1,...,t_k\in T und alle Funktionssymbole f aus \sum^+ (Bemerkung: dies ist wohldefiniert) Dann gilt tatsächlich A\Vdash\Delta^+.

Satz: Vollständigkeitssatz der Prädikatenlogik

Sei \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Dann gilt \Gamma\Vdash\varphi \Rightarrow \Gamma\vdash\varphi. Insbesondere ist jede allgemeingültige Formel ein Theorem.

Beweis:indirekt

• \Gamma\not\vdash\varphi
• \Gamma\cup\{\lnot\varphi\} konsistent
• \Gamma\cup\{\lnot\varphi\} erfüllbar
• \exists\Delta\supseteq\Gamma\cup\{\lnot\varphi\} maximal konsistent
• \exists\Delta^+\supseteq\Delta maximal konsistent mit Konkretisierungen
• \Delta^+ erfüllbar
• \Delta erfüllbar
• \Gamma\not\Vdash\varphi

Bemerkung

• Dieser Satz ist (im wesentlichen) der berühmte Gödelsche Vollständigkeitssatz von 1930.
• Der obige Beweis wurde von Leon Henkin 1949 veröffentlicht.

Wir haben gleichzeitig gezeigt:

Satz

Sei \Gamma höchstens abzählbar unendliche und konsistente Menge von Formeln. Dann hat \Gamma ein höchstens abzählbar unendliches Modell.

Beweis: \Gamma konsistent heißt \Gamma\not\vdash\bot. Obiger Beweis gibt ein Modell A von \Gamma\cup\{\lnot\bot\} an. Wir zeigen, dass diese Struktur A höchstens abzählbar unendlich ist:

• Sei \sum Signatur der Relations- und Funktionssymbole aus \Gamma.
• |\Gamma|\leq \mathbb{N}_0 \Rightarrow |\sum|\leq \mathbb{N}_0
• \Rightarrow |\sum_n|\leq \mathbb{N}_0 und |\Delta_n|\leq \mathbb{N}_0 für alle n\geq 0
• \Rightarrow |\sum^+|,|\Delta^+| \leq\mathbb{N}_0
• \Rightarrow |T| \leq\mathbb{N}_0
• \Rightarrow A hat \leq\mathbb{N}_0 viele Elemente
• \Rightarrow \Gamma\cup\{\lnot\bot\} hat ein höchstens abzählbar unendliches Modell
• \Rightarrow \Gamma hat ein höchstens abzählbar unendliches Modell

Vollständigkeit und Korrektheit für die Prädikatenlogik

Satz

Seien \Gamma eine Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel. Dann gilt \Gamma\vdash\varphi\Leftrightarrow \Gamma\Vdash\varphi. Insbesondere ist eine $\sum$-Formel genau dann allgemeingültig, wenn sie ein Theorem ist.

Beweis: Folgt unmittelbar aus Korrektheitssatz und Vollständigkeitssatz.

Folgerung 1: Kompaktheit

Satz

Seien \Gamma eine u.U. unendliche Menge von $\sum$-Formeln und \varphi eine $\sum$-Formel mit \Gamma\Vdash\varphi. Dann existiert \Gamma'\subseteq\Gamma endlich mit \Gamma'\Vdash\varphi.

Beweis: \Gamma\Vdash\varphi

• \Gamma\vdash\varphi (nach dem Vollständigkeitssatz)
• es gibt Deduktion von \varphi mit Hypothesen \gamma_1,...,\gamma_n\in\Gamma
• \Gamma′=\{\gamma_1,...,\gamma_n\}\subseteq\Gamma endlich mit \Gamma′\vdash\varphi
• \Gamma′\vdash\varphi (nach dem Korrektheitssatz).

Folgerung (Kompaktheits- oder Endlichkeitssatz)

Sei \Gamma eine u.U. unendliche Menge von $\sum$-Formeln. Dann gilt \Gamma erfüllbar \Leftrightarrow \forall\Gamma′\subseteq\Gamma endlich: \Gamma′ erfüllbar

Beweis:

• \Gamma unerfüllbar
• \Leftrightarrow \Gamma\cup\{\lnot\bot\} unerfüllbar
• \Leftrightarrow \Gamma\Vdash\bot
• \Leftrightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′\Vdash\bot
• \Leftrightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′\cup\{\lnot\bot\} unerfüllbar
• \Leftrightarrow es gibt \Gamma′\subseteq\Gamma endlich: \Gamma′ unerfüllbar

Satz

Sei \Delta eine u.U. unendliche Menge von $\sum$-Formeln, so dass für jedes n\in\mathbb{N} eine endliche Struktur A_n mit A_\Vdash\Delta existiert, die wenigstens n Elemente hat. Dann existiert eine unendliche Struktur A mit A\Vdash\Delta.

Beweis: für n\in\mathbb{N} setze \varphi_n=\exists x_1 \exists x_2 ...\exists x_n \bigwedge_{1\leq i< j \leq n} x_i \not= x_j

• und \Gamma =\Delta\cup\{\varphi_n | n\geq 0\}.
• Für \Gamma′\subseteq\Gamma endlich existiert n\in\mathbb{N} mit \varphi_m\not\in\Gamma′ für alle m\geq n
• \Rightarrow A_n\Vdash\Gamma′, d.h. jede endliche Teilmenge von \Gamma ist erfüllbar.
• \Rightarrow es gibt Struktur A mit A\Vdash\Gamma
• \Rightarrow A hat \geq n Elemente (für alle n\in\mathbb{N})

Folgerung 2: Löwenheim-Skolem

Frage: Gibt es eine Menge \Gamma von $\sum$-Formeln, so dass für alle Strukturen A gilt: A\Vdash\Gamma \Leftrightarrow A\cong (\mathbb{R},+,*, 0 , 1 )?

Satz von Löwenheim-Skolem

Sei \Gamma erfüllbare und höchstens abzählbar unendliche Menge von $\sum$-Formeln. Dann existiert ein höchstens abzählbar unendliches Modell von \Gamma.

Beweis:

• Gamma erfüllbar \Rightarrow \Gamma\not\Vdash\bot
• \Rightarrow \Gamma\not\vdash\bot, d.h. \Gamma konsistent
• \Rightarrow \Gamma hat ein höchstens abzählbar unendliches Modell.

Die Frage auf der vorherigen Folie muß also verneint werden:

• angenommen, \Gamma wäre eine solche Menge
• \Rightarrow |\Gamma|\leq \mathbb{N}_0
• \Rightarrow \Gamma hat ein höchstens abzählbar unendliches Modell A
• \Rightarrow A\not\cong (\mathbb{R},+,*, 0 , 1 )

Folgerung 3: Semi-Entscheidbarkeit

Satz

Die Menge der allgemeingültigen $\sum$-Formeln ist semi-entscheidbar.

Beweis:Sei$\varphi$ $\sum$-Formel. Dann gilt

• \varphi allgemeingültig
• \Leftrightarrow \varphi Theorem
• \Leftrightarrow Es gibt hypothesenlose Deduktion mit Konklusion \varphi

Ein Semi-Entscheidungsalgorithmus kann also folgendermaßen vorgehen: Teste für jede Zeichenkette w nacheinander, ob sie hypothesenlose Deduktion mit Konklusion \varphi ist. Wenn ja, so gib aus „\varphi ist allgemeingültig“. Ansonsten gehe zur nächsten Zeichenkette über.

Der Satz von Church

Jetzt zeigen wir, daß dieses Ergebnis nicht verbessert werden kann: Die Menge der allgemeingültigen $\sum$-Formeln ist nicht entscheidbar. Wegen \varphi allgemeingültig \Leftrightarrow\lnot\varphi unerfüllbar reicht es zu zeigen, dass die Menge der erfüllbaren Sätze nicht entscheidbar ist. Genauer zeigen wir dies sogar für „Horn-Formeln“:

Definition

Eine Horn-Formel ist eine Konjunktion von $\sum$-Formeln der Form \forall x_1 \forall x_2 ...\forall x_n((\lnot\bot \wedge\alpha_1\wedge\alpha_2\wedge...\wedge\alpha_m)\rightarrow\beta), wobei \alpha_1,...,\alpha_m und \beta atomare $\sum$-Formeln sind.

Unser Beweis reduziert die unentscheidbare Menge PCP auf die Menge der erfüllbaren Horn-Formeln.

Im folgenden sei also I=((u_1,v_1),(u_2,v_2),...,(u_k,v_k)) ein Korrespondenzsystem und A das zugrundeliegende Alphabet. Hieraus berechnen wir eine Horn-Formel \varphi_I, die genau dann erfüllbar ist, wenn I keine Lösung hat. Wir betrachten die Signatur \sum= (\Omega,Rel,ar) mit

• \Omega=\{e\}\cup\{f_a|a\in A\} mit ar(e) =0 und ar(f_a) =1 für alle a\in A.
• Rel=\{R\} mit ar(R)=2.

Zur Abkürzung schreiben wir f_{a_1 a_2 ...a_n} (x) für f_{a_1}(f_{a_2}(...(f_{a_n}(x))...)) für alle a_1,a_2,...,a_n\in A und n\geq 0 (insbes. steht f_{\epsilon}(x) für x).

Zunächst betrachten wir die folgende Horn-Formel \psi_I:

• \wedge \bigwedge_{1\leq j \leq k}^{R(e,e)} \forall x,y(R(x,y)\rightarrow R(f_{u_j}(x),f_{v_j}(y)))
• \wedge \bigwedge_{a\in A} \forall x(e=f_a(x)\rightarrow \bot)

Beispiel: Betrachte die $\sum$-Struktur A mit Universum U_A=A^*

• e^A=\epsilon
• f_a^A(u) =au
• R^A=\{(u_{i1} u_{i2} ...u_{in},v_{i1} v_{i2} ...v_{in})|n\geq 0 , 1\geq i_1,i_2,...,i_n\geq k\}
• Für u,v\in A^* gilt f_u^A(v) =uv.
• Dann gilt A\Vdash \psi_I.

Lemma

Angenommen, das Korrespondenzsystem I hat keine Lösung. Dann ist die Horn-Formel \varphi_I=\psi_I \wedge \forall x(R(x,x)\rightarrow x=e) erfüllbar.

Beweis: Sei A die obige Struktur mit A\Vdash\psi_I.

• Um A\Vdash\forall x(R(x,x)\rightarrow x=e) zu zeigen, sei w\in U_A beliebig mit (w,w)\in R^A.
• Die Definition von R^A sichert die Existenz von n\geq 0 und 1\leq i_1,i_2,...,i_n\leq k mit u_{i1} u_{i2}...u_{in}=w=v_{i1} v_{i2} ...v_{in}.
• Da I keine Lösung hat, folgt n=0 und damit w=\epsilon.

Lemma

Sei B Struktur mit B\Vdash\psi_I. Dann gilt (f_{u_{i_1} u_{i_2} ...u_{i_n}}^B (e^B),f_{v_{i_1} v_{i_2}...v_{i_n}}^B(e^B))\in R^B für alle n\geq 0, 1\leq i_1,i_2,...,i_n \leq k.

Beweis: per Induktion über n\geq 0.

• IA: für n=0 gelten f_{u_{i_1} u_{i_2} ...u_{i_n}}^B(e^B) =e^B und f_{v_{i_1} v_{i_2}...v_{i_n}}^B(e^B) =e^B
  • und damit (f_{u_{i_1} u_{i_2} ...u_{i_n}}^B(e^B), f_{v_{i_1} v_{i_2}...v_{i_n}}^B(e^B) \in R^B
  • wegen B\Vdash\psi_I.
• IS: Seien n>0 und 1\leq i_1 ,i_2 ,...,i_n\leq k.
  • Mit u=u_{i2} u_{i3} ...u_{in} und v=v_{i2} v_{i3} ...v_{in} gilt nach IV (f_u^B(e^B),f_v^B(e^B))\in R^B. Wegen B\Vdash\psi_I folgt f_{u_{i_1} u_{i_2} ...u_{i_n}}^B(e^B), f_{v_{i_1} v_{i_2}...v_{i_n}}^B(e^B) = (f_{u_{i1}}^B (f_u^B(e^B)),f_{v_{i1}}^B (f_v^B(e^B)))\in RB.

Lemma

Angenommen, (i_1,...,i_n) ist eine Lösung von I. Dann ist die $\sum$-Formel \varphi_I unerfüllbar.

Satz

Die Menge der unerfüllbaren Horn-Formeln ist nicht entscheidbar.

Beweis: Die Abbildung I\rightarrow\varphi_I ist berechenbar.

Nach den vorherigen Lemmata ist sie eine Reduktion von PCP auf die Menge der unerfüllbaren Horn-Formeln. Da PCP unentscheidbar ist (vgl. Automaten, Sprachen und Komplexität), ist die Menge der unerfüllbaren Horn-Formeln unentscheidbar.

Folgerung (Church 1936)

Die Menge der allgemeingültigen $\sum$-Formeln ist nicht entscheidbar.

Beweis: Eine $\sum$-Formel \varphi ist genau dann unerfüllbar, wenn \lnot\varphi allgemeingültig ist. Also ist \varphi\rightarrow\lnot\varphi eine Reduktion der unentscheidbaren Menge der unerfüllbaren $\sum$-Formeln auf die Menge der allgemeingültigen $\sum$-Formeln, die damit auch unentscheidbar ist.

Allgemeingültige $\sum$-Formeln gelten in allen Strukturen. Was passiert, wenn wir uns nur auf „interessante“ StrukturenAeinschränken (z.B. auf eine konkrete), d.h. wenn wir die Theorie Th(A) von A betrachten?

Theorie der natürlichen Zahlen

Definition

Sei A eine Struktur. Dann ist Th(A) die Menge der prädikatenlogischen $\sum$-Formeln \varphi mit A\Vdash\varphi. Diese Menge heißt die(elementare) Theorie von A.

Beispiel: Sei N= (N,\leq,+,*, 0 , 1 ). Dann gelten

• (\forall x\forall y:x+y=y+x)\in Th(N)
• (\forall x\exists y:x+y= 0 )\not\in Th(N)
• aber (\forall x\exists y:x+y= 0 )\in Th((Z,+, 0 )).

Lemma

Die Menge Th(N) aller Sätze \varphi mit N\Vdash\varphi ist nicht entscheidbar.

Zahlentheoretisches Lemma

Für alle n\in N,x_0,x_1,...,x_n\in N existieren c,d\in N, so dass für alle 0\leq i\leq n gilt: x_i=c\ mod ( 1 +d*(i+ 1 )).

Beweis:Setze m= max\{n,x_0,x_1 ,...,x_n\} und d=2*3*4...(m+1). Dann sind die Zahlen 1+d, 1+d*2,..., 1 +d*(n+1) paarweise teilerfremd. Nach dem Chinesischen Restsatz folgt die Existenz einer natürlichen Zahl c.

Bemerkung: Es gibt $\sum$-Formeln

• mod(x_1,x_2 ,y) mit N\Vdash_{\alpha} mod \Leftrightarrow \alpha (x_1) mod\alpha (x_2) =\alpha (y).
• γ(x_1 ,x_2 ,x_3 ,y) mit N\Vdash_{\alpha} γ\Leftrightarrow \alpha(x_1) mod(1+\alpha(x_2)*(\alpha (x3)+1)) =\alpha (y).

Satz

Sei A eine Struktur, so dass Th(A) semi-entscheidbar ist. Dann ist Th(A) entscheidbar.

Korollar Die Menge TH(N) der Aussagen \varphi mit N\Vdash\varphi ist nicht semi-entscheidbar.

Korollar (1. Gödelscher Unvollständigkeitssatz)

Sei Gamma eine semi-entscheidbare Menge von Sätzen mit N\Vdash\gamma für alle \gamma\in\Gamma. Dann existiert ein Satz \varphi mit \Gamma\not\vdash\varphi und \Gamma\not\vdash\lnot\varphi (d.h. "\Gamma ist nicht vollständig").

2. Semi Entscheidungsverfahren für allgemeingültige Formeln

bekanntes Verfahren mittels natürlichem Schließen: Suche hypothesenlose Deduktion mit Konklusion \psi.

Jetzt alternatives Verfahren, das auf den Endlichkeitssatz der Aussagenlogik zurückgreift:

• Berechne aus $\sum$-Formel \psi eine Menge E von aussagenlogischen Formeln mit E unerfüllbar \Leftrightarrow\lnot\psi unerfüllbar \Leftrightarrow\psi allgemeingültig
• Suche endliche unerfüllbare Teilmenge E' von E

Kern des Verfahrens ist es also, aus $\sum$-Formel \varphi eine Menge E aussagenlogischer Formeln zu berechnen mit \varphi unerfüllbar \Leftrightarrow E unerfüllbar.

Hierzu werden wir die Formel \varphi zunächst in zwei Schritten (Gleichungsfreiheit und Skolem-Form) vereinfachen, wobei die Formel erfüllbar bzw unerfüllbar bleiben muss.

Definition

Zwei $\sum$-Formeln \varphi und \psi heißen erfüllbarkeitsäquivalent, wenn gilt: \varphi ist erfüllbar \Leftrightarrow\psi ist erfüllbar

Unsere Vereinfachungen müssen also erfüllbarkeitsäquivalente Formeln liefern.

Elimination von Gleichungen

Definition

Eine $\sum$-Formel ist gleichungsfrei, wenn sie keine Teilformel der Form s=t enthält.

Ziel: aus einer \sum Formel \varphi soll eine erfüllbarkeitsäquivalente gleichungsfreue Formel \varphi' berechnet werden

Bemerkung: Man kann i.a. keine äquivalente gleichungsfreie Formel \varphi' angeben, da es eine solche z.B. zu \varphi=(\forall x\forall y:x=y) nicht gibt.

Idee: Die Formel \varphi' entsteht aus \varphi, indem alle Teilformeln der Form x=y durch GI(x,y) ersetzt werden, wobei GI ein neues Relationssymbol ist.

Notationen

• Sei \sum=(\Omega,Rel,ar) endliche Signatur und \varphi $\sum$-Formel
• \sum_{GI} = (\Omega, Rel\bigcup^+\{GI\},ar_{GI}) mit ar_{GI}(f) für alle f\in\Omega\cup Rel und ar_{GI}(GI)=2
• Für eine $\sum$-Formel \varphi bezeichnet \varphi_{GI} die $\sum_{GI}$-Formel, die aus \varphi entsthet, indem alle Vorkommen und Teilformen s=t durch GI(s,t) ersetzt werden.

Behauptung: \varphi erfüllbar \Rightarrow \varphi_{GI} erfüllbar

Behauptung: es gilt nicht \varphi erfüllbar \Leftarrow\varphi_{GI} erfüllbar

Definition

Sei A eine $\sum$-Struktur und \sim eine binäre Relation auf U_A. Die Relation \sim heißt Kongruenz auf A, wenn gilt:

• \sim ist eine Äquivalentrelation (d.h. reflexiv, transitiv und symmetrisch)
• für alle f\in\Omega mit k=ar(f) und alle a_1,b_1,...,a_k,b_k\in U_A gilt a_1\sim b_1,a_2\sim b_2,...,a_k\sim b_k\Rightarrow f^A(a_1,...,a_k)\sim f^A(b_1,...,b_k)
• für alle R\in Rel mit k=ar(R) und alle a_1,b_1,...,a_k,b_k\in U_A gilt a_1\sim b_1,...,a_k\sim b_k,(a_1,...,a_k)\in R^A\Rightarrow (b_1,...,b_k)\in R^A.

Definition

Sei A eine $\sum$-Struktur und \sim eine Kongruenz auf A.

1. Für a\in U_A sei [a]=\{b\in U_A|a\sim b\} die Äquivalenzklasse von a bzgl \sim.
2. Dann definieren wir den Quotienten B=A\backslash \sim von A bzgl \sim wie folgt:

• U_B=U_A\backslash\sim = \{[a]|a\in U_A\}
• Für jedes f\in\Omega mit ar(f)=k und alle a_1,...,a_k\in\U_A setzten wir f^B([a_1],...,[a_k])=[f^A(a_1,...,a_k)]
• für jede R\in Rel mit ar(R)=k setzten wir R^B=\{([a_1],[a_2],...,[a_k])|(a_1,...,a_k)\in R^A\}

3. Sei p:Var\rightarrow U_A Variableninterpretation. Dann definieren die Variableninterpretation p\backslash\sim: Var\rightarrowU_B:x\rightarrow[p(x)].

Veranschaulichung:

Lemma 1

Sei A Struktur, p:Var\rightarrow U_A Variableninterpretation und \sim Kongruenz. Seien weiter B=A\backslash\sim und p_B=p\backslash\sim. Dann gilt für jeden Term :[p(t)]=p_B(t)

Beweis: per Induktion über den Aufbau des Terms t

Lemma 2

Sei A $\sum$-Struktur, \sim Kongruenz und B=A\backslash\sim. Dann gilt für alle R\in Rel mit k=ar(R) und alle c_1,...,c_k\in U_A: ([c_1],[c_2],...,[c_k])\in R^B\Leftrightarrow (c_1,c_2,...,c_k)\in R^A

Satz

Seien A $\sum_{GI}$-Struktur und p:Var\rightarrow U_A Variableninterpretation, so dass \sim=GI^A Kongruenz auf A ist. Seien B=A\backslash\sim und p_B=p\backslash\sim. Dann gilt für alle $\sum$-Formeln \varphi: A\Vdash_p \varphi_{GI} \Leftrightarrow B\Vdash_{p_B} \varphi

Beweis: per Induktion über den Aufbau der Formel \varphi

Lemma

Aus einer endlichen Signatur \sum kann ein gleichungsfreuer Horn-Satz Kong_{\sum} über \sum_{GI} berechnet werden, so dass für alle $\sum_{GI}$-Strukturen A gilt: A\Vdash Kong_{\sum} \Leftrightarrow GI^A ist eine Kongruenz

Satz

Aus einer endlichen Signatur \sum und einer $\sum$-Formel \varphi kann eine gleichungsfreie und erfüllbarkeitsäquivalente $\sum_{GI}$-Formel \varphi' berechnet werden. Ist \varphi Horn Formel, so ist auch \varphi' Horn Formel.

Beweis: Setzte \varphi' =\varphi_{GI}\wedge Kong_{\sum} und zeige: \varphi erfüllbar \Leftrightarrow \varphi' erfüllbar.

Skolemform

Ziel: Jede $\sum$-Formel \varphi ist erfüllbarkeitsäquivalent zu einer $\sum$′-Formel \varphi′=\forall x_1\forall x_2 ...\forall x_k \psi, wobei \psi kein Quantoren enthält, \varphi′ heißt in Skolemform.

Bemerkung: Betrachte die Formel \exists x\exists y E(x,y). Es gibt keine Formel in Skolemform, die hierzu äquivalent ist.

2 Schritte:

1. Quantoren nach vorne (d.h. Pränexform)
2. Existenzquantoren eliminieren

Definition

Zwei $\sum$-Formeln \varphi und \psi sind äquivalent (kurz:$\varphi\equiv\psi$), wenn für alle $\sum$-Strukturen A und alle Variableninterpretationen \rho gilt: $A\Vdash_\rho\psi \Lefrightarrow \Leftrightarrow A\Vdash_\rho\psi$.

Lemma

Seien Q\in\{\exists ,\forall\} und \oplus\in\{\wedge,\vee,\rightarrow,\leftarrow\}. Sei \varphi= (Qx \alpha)\oplus\beta und sei y eine Variable, die weder in \alpha noch in \beta vorkommt. Dann gilt \varphi \equiv \begin{cases} Qy(\alpha[x:=y]\oplus\beta) \text{ falls } \oplus\in\{\wedge,\vee,\leftarrow\}\\ \forall y(\alpha[x:=y]\rightarrow\beta) \text{ falls } \oplus=\rightarrow,Q=\exists \\ \exists y(\alpha[x:=y]\rightarrow\beta) \text{ falls }\oplus=\rightarrow,Q=\forall\end{cases}

Notwendigkeit der Bedingung „y kommt weder in \alpha noch in \beta vor“:

• (\exists x:f(x) \not =f(y))\wedge\beta \not\equiv\exists y: (f(y) \not =f(y)\wedge\beta)
• (\exists x:\lnot P(x))\wedge P(y)\not\equiv \exists y: (\lnot P(y) \wedge P(y))

Lemma

Seien Q\in\{\exists,\forall\} und \oplus\in\{\wedge,\vee,\rightarrow,\leftarrow\}. Sei \varphi= (Qx\alpha)\oplus\beta und sei y eine Variable, die weder in \alpha noch in \beta vorkommt. Dann gilt \varphi\equiv\begin{cases} Qy(\alpha[x:=y]\oplus\beta) \text{ falls }\oplus\in\{\wedge,\vee,\leftarrow\} \\ \forall y(\alpha[x:=y]\rightarrow\beta) \text{ falls }\oplus=\rightarrow,Q=\exists \\ \exists y(\alpha[x:=y]\rightarrow\beta) \text{ falls }\oplus=\rightarrow,Q=\forall \end{cases}

Beweis: (für den Fall Q=\exists und \oplus=\wedge)

• Seien A $\sum$-Struktur und \rho Variableninterpretation.
• Für a\in U_A setze \rho_a:=\rho[y\rightarrow a].
• Dann gilt \rho_a[x\rightarrow \rho_a(y)](z) =\rho[x\rightarrow a](z) für alle z\not=y

Wir erhalten also

• A\vdash_\rho (\exists x\alpha)\wedge\beta
• \Leftrightarrow A\vdash_\rho (\exists x\alpha) und A\vdash_\rho \beta
• \Leftrightarrow (es gibt a\in U_A mit A\vdash_{\rho[x\rightarrow a]}\alpha) und (es gilt A\vdash_\rho \beta)
• \Leftrightarrow es gibt a\in U_A mit (A\vdash_{\rho[x\rightarrow a]}\alpha und A\vdash_\rho \beta)
• \Leftrightarrow es gibt a\in U_A mit
  • A\vdash_{\rho_a[x\rightarrow \rho_a(y)]}\alpha (da y in \alpha nicht vorkommt)
  • A\vdash_{\rho_a} \beta (da y in \beta nicht vorkommt)
• \Leftrightarrow es gibt a\in U_A mit
  • A\vdash_{\rho_a} \alpha[x:=y]
  • A\vdash_{\rho_a} \beta
• \Leftrightarrow es gibt a\in U_A mit A\vdash_{\rho[y\rightarrow a]}\alpha[x:=y]\wedge\beta
• \Leftrightarrow A\vdash_\rho \exists y(\alpha[x:=y]\wedge\beta)

Satz

Aus einer endlichen Signatur \sum und einer $\sum$-Formel \varphi kann eine äquivalente $\sum$-Formel \varphi′=Q_1 x_1 Q_2 x_2 ...Q_k x_k \psi (mit Q_i\in\{\exists,\forall\},\psi quantorenfrei und x_i paarweise verschieden) berechnet werden. Eine Formel \varphi′ dieser Form heißt Pränexform. Ist \varphi gleichungsfrei, so ist auch \varphi′ gleichungsfrei.

Beweis: Der Beweis erfolgt induktiv über den Aufbau von \varphi:

• I.A. \varphi ist atomare Formel: Setze \varphi′=\varphi.
• I.S.
  • \varphi=\lnot\psi : Nach I.V. kann Formel in Pränexform \psi\equiv Q_1 x_1 Q_2 x_2 ...Q_m x_m \psi′ berechnet werden. Mit \forall=\exists und \exists=\forall setze \varphi′=Q_1 x_1 Q_2 x_2 ...Q_m x_m\lnot\psi′.
  • \varphi=\exists x\psi: Nach I.V. kann Formel in Pränexform \psi\equiv Q_1 x_1 Q_2 x_2 ...Q_m x_m \psi′ berechnet werden. Setze \varphi′= \begin{cases} \exists x Q_1 x_1 Q_2 x_2 ...Q_m x_m\psi′\text{ falls }x\not\in\{x_1,x_2,...,x_m\}\\ Q_1 x_1 Q_2 x_2 ...Q_m x_m\psi′\text{ sonst}\end{cases}
  • \varphi=\alpha\wedge\beta: Nach I.V. können Formeln in Pränexform \alpha\equiv Q_1 x_1 Q_2 x_2 ...Q_mx_m \alpha_0; \beta\equiv Q_1′y_1 Q_2′y_2 ...Q_n′y_n \beta_0 berechnet werden.

Ziel: Berechnung einer erfüllbarkeitsäquivalenten Formel in Skolemform

Idee:

1. wandle Formel in Pränexform um
2. eliminiere $\exists$-Quantoren durch Einführen neuer Funktionssymbole

Konstruktion: Sei \varphi=\forall x_1\forall x_2...\forall x_m\exists y\psi Formel in Pränexform (u.U. enthält \psi weitere Quantoren). Sei g\not\in\Omega ein neues m-stelliges Funktionssymbol. Setze \varphi′=\forall x_1\forall x_2...\forall x_m \psi[y:=g(x_1,...,x_m)]. Offensichtlich hat $\varphi$′einen Existenzquantor weniger als \varphi. Außerdem ist \varphi′ keine $\sum$-Formel (denn sie verwendet g\not\in\Omega), sondern Formel über einer erweiterten Signatur.

Lemma

Die Formeln \varphi und \varphi′ sind erfüllbarkeitsäquivalent.

Beweis: „$\Leftarrow$“ Sei A′ Struktur und \rho′ Variableninterpretation mit A′\vdash_{\rho′}\varphi′. Wir zeigen A′\vdash_{\rho′}\varphi. Hierzu seien a_1,...,a_m\in U_{A′} beliebig.

Satz

Aus einer Formel \varphi kann man eine erfüllbarkeitsäquivalente Formel \varphi in Skolemform berechnen. Ist \varphi gleichungsfrei, so auch \varphi.

Beweis: Es kann zu \varphi äquivalente Formel \varphi_0 =Q_1 x_1 Q_2 x_2 ...Q_{\iota} x_{\iota} \psi in Pränexform berechnet werden (mit n\leq {\iota} Existenzquantoren). Durch wiederholte Anwendung des vorherigen Lemmas erhält man Formeln \varphi_1,\varphi_2,...\varphi_n mit

• \varphi_i und \varphi_{i+1} sind erfüllbarkeitsäquivalent
• \varphi_{i+1} enthält einen Existenzquantor weniger als \varphi_i
• \varphi_{i+1} ist in Pränexform
• ist \varphi_i gleichungsfrei, so auch \varphi_{i+1}

Dann ist \bar{\varphi}=\varphi_n erfüllbarkeitsäquivalente (ggf. gleichungsfreie) Formel in Skolemform.

Herbrand-Strukturen und Herbrand-Modelle

Sei \sum= (\Omega,Rel,ar) eine Signatur. Wir nehmen im folgenden an, dass \Omega wenigstens ein Konstantensymbol enthält.

Das Herbrand-Universum D(\sum) ist die Menge aller variablenfreien $\sum$-Terme.

Beispiel: \Omega =\{b,f\} mit ar(b) =0 und ar(f) =1. Dann gilt D(\sum) =\{b,f(b),f(f(b)),f(f(f(b))),...\}

Eine $\sum$-Struktur A=(UA,(fA)f\in\Omega,(RA)R\in Rel) ist eine Herbrand-Struktur, falls folgendes gilt:

1. UA=D(\sum),
2. für alle f\in\Omega mit ar(f)=k und alle t_1,t_2,...,t_k\in D(\sum) ist f^A(t_1,t_2,...,t_k) =f(t_1,t_2,...,t_k).

Für jede Herbrand-Struktur A, alle Variableninterpretationen \rho und alle variablenfreien Terme t gilt dann \rho(t) =t.

Ein Herbrand-Modell von \varphi ist eine Herbrand-Struktur, die gleichzeitig ein Modell von \varphi ist.

Satz

Sei \varphi eine gleichungsfreie Aussage in Skolemform. \varphi ist genau dann erfüllbar, wenn \varphi ein Herbrand-Modell besitzt.

Beweis:

• Falls \varphi ein Herbrand-Modell hat, ist \varphi natürlich erfüllbar.
• Sei nun \varphi=\forall y_1...\forall y_n\psi erfüllbar. Dann existieren eine $\sum$-Struktur A=(U_A,(f^A)_{f\in\Omega},(R^A)_{R\in Rel}) und eine Variableninterpretation \rho mit A\vdash_\rho \varphi.

Plan des Beweises

Wir definieren eine Herbrand-Struktur B=(D(\sum),(f^B)_{f\in\Omega},(R^B)_{R\in Rel}):

• Seien f\in\Omega mit ar(f)=k und t_1,...,t_k\in D(\sum). Um eine Herbrand-Struktur B zu konstruieren setzen wir f^B(t_1,...,t_k) =f(t_1,...,t_k)
• Sei R\in Rel mit ar(R)=k und seien t_1,...,t_k\in D(\sum). Dann setze (t_1,...,t_k)\in RB:\Leftrightarrow (\rho(t_1),...,\rho(t_k))\in RA.

Sei \rho_B:Var \rightarrow D(\sum) beliebige Variableninterpretation.

Behauptung 1:

Ist \psi eine quantoren- und gleichungsfreie Aussage, so gilt A\vdash_\rho\psi \Leftrightarrow B\vdash_{\rhoB} \psi. Diese Behauptung wird induktiv über den Aufbau von \psi gezeigt.

Intermezzo

Behauptung 1 gilt nur für quantorenfreie Aussagen

\sum = (\Omega,Rel,ar) mit \Omega =\{a\},ar(a) =0 und Rel=\{E\},ar(E) =2. Betrachte die Formel \varphi=\forall x(E(x,x)\wedge E(a,a)) in Skolemform. A\vdash_\rho \varphi mit U^A=\{a^A,m\} und E^A=\{(m,m),(a^A,a^A)\}. Die konstruierte Herbrand-Struktur B:U_B=D(\sum) =\{a\} und E^B=\{(a,a)\}.

Betrachte nun die Formel \psi=\forall x,y E(x,y). Dann gilt B\vdash_{\rhoB}\psi und A\not\vdash_\rho \psi.

Für allgemeine Formeln in Skolemform (also u.U. mit Quantoren) können wir also Behauptung 1 nicht zeigen, sondern höchstens die folgende Abschwächung.

Behauptung 2:

Ist \psi eine gleichungsfreie Aussage in Skolemform, so gilt A\vdash_\rho \psi \Rightarrow B\vdash_{\rhoB}\psi. (hieraus folgt dann B\vdash_{\rhoB}\varphi wegen A\vdash_\rho \varphi)

Diese Behauptung wird induktiv über die Anzahl n der Quantoren in \psi bewiesen.

Die Herbrand-Expansion

verbleibende Frage: Wie erkennt man, ob eine gleichungsfreie Aussage in Skolemform ein Herbrand-Modell hat?

Beispiel: Seien \sum=(\{a,f\},\{P,R\},ar) und \varphi=\forall x\forall y (P(a,x)\wedge\lnot R(f(y)))$. Jedes Herbrand-Modell A von \varphi

• hat als Universum das Herbrand-Universum D(\sum)=\{a,f(a),f^2 (a),...\}=\{f^n(a)|n\geq 0\}
• erfüllt f^A(f^n(a))= f^{n+1} (a) für alle n\geq 0

Um ein Herbrand-Modell zu konstruieren, müssen (bzw. können) wir für alle Elemente s,t,u\in D(\sum) unabhängig und beliebig wählen, ob (s,t)\in P^A und u\in R^A gilt. Wir fassen dies als „aussagenlogische B-Belegung“ B der „aussagenlogischen atomaren Formeln“ P(s,t) bzw. R(u) auf.

Jede solche aussagenlogische B-Belegung B definiert dann eine Herbrand-Struktur A_B:

• P^{A_B} = \{(s,t)\in D(\sum)^2 |B(P(s,t))= 1\}
• R^{A_B} = \{u\in D(\sum) |B(R(u))= 1\}

Mit \varphi=\forall x\forall y(P(a,x)\wedge\lnot R(f(y))) gilt dann A_B \Vdash_\rho \varphi

• \Leftrightarrow A_B \Vdash_{\rho[x\rightarrow f^m(a)][y\rightarrow f^n(a)]} P(a,x)\wedge\lnot R(f(y)) f.a. m,n\geq 0
• \Leftrightarrow (a,fm(a))\in P^{A_B} und f^{n+1}(a)\not\in R^{A_B} f.a. m,n\geq 0
• \Leftrightarrow B(P(a,f^m(a)))= 1 und B(R(f^{n+1} (a)))= 0 f.a. m,n\geq 0
• \Leftrightarrow B(P(a,f^m(a))\wedge\lnot R(f^{n+1} (a)))= 1 f.a. m,n\geq 0

Also hat \varphi genau dann ein Herbrand-Modell, wenn es eine erfüllende B-Belegung B der Menge aussagenlogischer Formeln E(\varphi)=\{P(a,f^m(a))\wedge\lnot R(f^{n+1}(a)) | m,n\geq 0\} gibt.

Beispiellösung: Setzt B(P(s,t))= 1 und B(R(s))= 0 für alle s,t\in D(\sum).

Diese B-Belegung erfüllt E(\varphi) und „erzeugt“ die Herbrand-Struktur A_B mit P^{A_B}=D(\sum)^2 und R^{A_B}=\varnothing.

Nach obiger Überlegung gilt A_B\Vdash\varphi, wir haben also ein Herbrand-Modell von \varphi gefunden.

Sei \varphi=\forall y_1\forall y_2...\forall y_n\psi gleichungsfreie Aussage in Skolemform.

Ziel: Konstruktion einer Menge aussagenlogischer Formeln, die genau dann erfüllbar ist, wenn \varphi ein Herbrand-Modell hat.

Die Herbrand-Expansion von \varphi ist die Menge der Aussagen E(\varphi)=\{\psi[y_1:=t_1][y_2:=t_2]...[y_n:=t_n]|t_1,t_2,...,t_n\in D(\sum)\}

Die Formeln von E(\varphi) entstehen also aus \psi, indem die (variablenfreien) Terme aus D(\sum) in jeder möglichen Weise in \psi substituiert werden.

Wir betrachten die Herbrand-Expansion von \varphi im folgenden als eine Menge von aussagenlogischen Formeln.

Die atomaren Formeln sind hierbei von der Gestalt P(t_1,...,t_k) für P\in Rel mit ar(P)=k und t_1,...,t_k\in D(\sum).

Konstruktion

Sei B:\{P(t_1,...,t_k)|P\in Rel,k=ar(P),t_1,...,t_k\in D(\sum)\}\rightarrow B eine B-Belegung. Die hiervon induzierte Herbrand-Struktur A_B ist gegeben durch P^{A_B} = \{(t_1,...,t_k)|t_1,...,t_k\in D(\sum),B(P(t_1,...,t_k))= 1\} für alle P\in Rel mit ar(P)=k.

Lemma

Für jede quantoren- und gleichungsfreie Aussage \alpha und jede Variableninterpretation \rho in A_B gilt A_B\Vdash_\rho\alpha \Leftrightarrow B(\alpha)= 1.

Beweis:

• per Induktion über den Aufbau von \alpha
• I.A. \alpha ist atomar, d.h. \alpha= P(t_1,...,t_k) mit t_1,...,t_k variablenlos A_B\Vdash_\rho \alpha\Leftrightarrow (\rho(t_1),\rho(t_2),...,\rho(t_k))\in P^{A_B}\Leftarrow B(\alpha)= 1
• I.S.
  • \alpha=\beta\wedge\gamma: A_B\Vdash_\rho \alpha\Leftrightarrow A_B \Vdash_\rho\beta und A_B\Vdash_\rho\gamma \Leftrightarrow B(\beta)=B(\gamma)= 1 \Leftrightarrow B(\alpha)= 1
  • \alpha=\beta\vee\gamma: analog
  • \alpha=\beta\rightarrow\gamma: analog
  • \alpha=\lnot\beta: analog

Lemma

Sei \varphi=\forall y_1 \forall y_2 ...\forall y_n\psi gleichungsfreie Aussage in Skolemform. Sie hat genau dann ein Herbrand-Modell, wenn die Formelmenge E(\varphi) (im aussagenlogischen Sinn) erfüllbar ist.

Beweis: Seien A Herbrand-Struktur und \rho Variableninterpretation. Sei B die B-Belegung mit B(P(t_1,...,t_k))= 1\Leftrightarrow(t_1,...,t_k)\in P^A für alle P\in Rel mit k=ar(P) und t_1,...,t_k\in D(\sum). Dann gilt A=A_B.

Satz von Gödel-Herbrand-Skolem

Sei \varphi gleichungsfreie Aussage in Skolemform. Sie ist genau dann erfüllbar, wenn die Formelmenge E(\varphi) (im aussagenlogischen Sinn) erfüllbar ist.

Beweis: \varphi erfüllbar \Leftrightarrow \varphi hat ein Herbrand-Modell \Leftrightarrow E(\varphi) ist im aussagenlogischen Sinne erfüllbar.

Satz von Herbrand

Eine gleichungsfreie Aussage \varphi in Skolemform ist genau dann unerfüllbar, wenn es eine endliche Teilmenge von E(\varphi) gibt, die (im aussagenlogischen Sinn) unerfüllbar ist.

(Jacques Herbrand (1908-1931))

Beweis: \varphi unerfüllbar \Leftrightarrow E(\varphi) unerfüllbar \Leftrightarrow es gibt M\subseteq E(\varphi) endlich und unerfüllbar

Algorithmus von Gilmore

Sei \varphi gleichungsfreie Aussage in Skolemform und sei \alpha_1,\alpha_2,\alpha_3,... eine Aufzählung von E(\varphi).

Eingabe: \varphi

n:=0;
repeat n := n +1;
until { alpha_1, alpha_2,..., alpha_n } ist unerfüllbar;
  (dies kann mit Mitteln der Aussagenlogik, z.B. Wahrheitswertetabelle, getestet werden)
Gib „unerfüllbar“ aus und stoppe.

Folgerung: Sei \varphi eine gleichungsfreie Aussage in Skolemform. Dann gilt:

• Wenn die Eingabeformel \varphi unerfüllbar ist, dann terminiert der Algorithmus von Gilmore und gibt „unerfüllbar“ aus.
• Wenn die Eingabeformel \varphi erfüllbar ist, dann terminiert der Algorithmus von Gilmore nicht, d.h. er läuft unendlich lange.

Beweis: unmittelbar mit Satz von Herbrand

Zusammenfassung: alternative Semi-Entscheidungsverfahren für die Menge der allgemeingültigen Formeln.

• Berechne aus \psi eine zu \lnot\psi erfüllbarkeitsäquivalente gleichungsfreie Formel \varphi in Skolemform.
• Suche mit dem Algorithmus von Gilmore nach einer endlichen Teilmenge E′ von E(\varphi), die unerfüllbar ist.

Berechnung von Lösungen

Beispiel

• \gamma = \forall x,y (R(x,f(y))\wedge R(g(x),y))
• \varphi = \forall x,yR(x,y)
• Gilt \{\gamma\}\Vdash\varphi? nein, denn A\Vdash\gamma\wedge\lnot\varphi mit
  • A=(\mathbb{N},f^A,g^A,R)
  • f^A(n)=g^A(n)=n+1$ für alle n\in\mathbb{N}
  • R^A = \mathbb{N}^2 \backslash\{( 0 , 0 )\}
• Gibt es variablenfreie Terme s und t mit \{\gamma\}\Vdash R(s,t)?
  • ja: z.B. (s,t)=(g(f(a)),g(a)) oder (s,t)=(g(a),g(a)) oder (s,t)=(a,f(b))
• Kann die Menge aller Termpaare (s,t) (d.h. aller „Lösungen“) mit \{\gamma\}\Vdash R(s,t) effektiv und übersichtlich angegeben werden?
  • Wegen \{\gamma\}\Vdash R(s,t) \Leftrightarrow\gamma\wedge\lnot R(s,t) unerfüllbar ist die gesuchte Menge der variablenfreien Terme (s,t) semi-entscheidbar, d.h. durch eine Turing-Maschine beschrieben.
• Im Rest des Logikteils der Vorlesung „Logik und Logikprogrammierung“ wollen wir diese Menge von Termpaaren „besser“ beschreiben (zumindest in einem Spezialfall, der die Grundlage der logischen Programmierung bildet).

Erinnerung

Eine Horn-Klausel der Prädikatenlogik ist eine Aussage der Form \forall x_1\forall x_2...\forall x_n ((\lnot\bot\wedge\alpha_1 \wedge\alpha_2 \wedge...\wedge\alpha_m)\rightarrow\beta), mit m\geq 0, atomaren Formeln \alpha_1,...,\alpha_m und \beta atomare Formel oder \bot.

Aufgabe: \varphi_1,...,\varphi_n gleichungsfreie Horn-Klauseln, \psi(x_1,x_2,...,x_{\iota} )=R(t_1,...,t_k) atomare Formel, keine Gleichung. Bestimme die Menge der Tupel (s_1,...,s_{\iota} ) von variablenfreien Termen mit \{\varphi_1,...,\varphi_n\}\Vdash\psi(s_1,...,s_{\iota} )=R(t_1,...,t_k)[x_1:=s_1]...[x_{\iota} :=s_{\iota} ], d.h., für die die folgende Formel unerfüllbar ist: \bigwedge_{1\leq i\leq n} \varphi_i \wedge \lnot\psi(s_1,...,s_{\iota} ) \equiv \bigwedge_{1\leq i\leq n} \varphi_i\wedge(\psi(s_1,...,s_{\iota} )\rightarrow\bot)

Erinnerung

• Eine Horn-Formel der Prädikatenlogik ist eine Konjunktion von Horn-Klauseln der Prädikatenlogik.
• Eine Horn-Klausel der Aussagenlogik ist eine Formel der Form (\lnot\bot\wedge q_1\wedge q_2 \wedge...\wedge q_m)\rightarrow r mit m\geq 0, atomaren Formeln q_1,q_2,...,q_m, r atomare Formel od. \bot.

Beobachtung

• Wir müssen die Unerfüllbarkeit einer gleichungsfreien Horn-Formel der Prädikatenlogik testen.
• Ist \varphi gleichungsfreie Horn-Klausel der Prädikatenlogik, so ist E(\varphi) eine Menge von Horn-Klauseln der Aussagenlogik.

Schreib- und Sprechweise

• \{\alpha_1,\alpha_2,...,\alpha_n\}\rightarrow\beta für Horn-Klausel der Prädikatenlogik (\lnot\bot\wedge\alpha_1 \wedge\alpha_2\wedge...\wedge\alpha_n)\rightarrow\beta insbes. \varnothing\rightarrow\beta für \lnot\bot\rightarrow\beta
• \{(N_i\rightarrow\beta_i) | 1\leq i\leq m\} für Horn-Formel \bigwedge_{1\leq i\leq m} (N_i\rightarrow\beta_i)

Folgerung: Sei \varphi =\bigwedge_{1\leq i\leq n} \varphi_i gleichungsfreie Horn-Formel der Prädikatenlogik. Dann ist \varphi genau dann unerfüllbar, wenn \bigcup_{1\leq i\leq n} E(\varphi_i) im aussagenlogischen Sinne unerfüllbar ist.

Beweis: Für 1\leq i\leq n sei \varphi_i=\forall x_1^i,x_2^i,...,x_{m_i}^i \psi_i. Zur Vereinfachung nehme wir an, daß die Variablen x_j^i für 1\leq i\leq n und 1\leq j\leq m_i paarweise verschieden sind.

Folgerung: Eine gleichungsfreie Horn-Formel der Prädikatenlogik \varphi=\bigwedge_{1\leq i\leq n} \varphi_i ist genau dann unerfüllbar, wenn es eine SLD-Resolution (M_0\rightarrow\bot,M_1\rightarrow\bot,...,M_m\rightarrow\bot) aus \bigcup_{1\leq i\leq n} E(\varphi_i) mit M_m =\varnothing gibt.

Substitutionen

Eine verallgemeinerte Substitution \sigma ist eine Abbildung der Menge der Variablen in die Menge aller Terme, so daß nur endlich viele Variable x existieren mit \sigma(x) \not=x.

Sei Def(\sigma)=\{x\ Variable|x\not =\sigma(x)\} der Definitionsbereich der verallgemeinerten Substitution \sigma. Für einen Term t definieren wir den Term t\sigma (Anwendung der verallgemeinerten Substitution \sigma auf den Term t) wie folgt induktiv:

• x\sigma=\sigma(x)
• [f(t_1 ,... ,t_k)]\sigma=f(t_1\sigma,... ,t_k\sigma) für Terme t_1,... ,t_k,f\in\Omega und $k=ar(f)$ Für eine atomare Formel \alpha=P(t_1 ,... ,t_k) (d.h. P\in Rel,ar(P) =k,t_1 ,... ,t_k Terme) sei \alpha\sigma = P(t_1\sigma,... ,t_k\sigma)

Verknüpfungvon verallgemeinerten Substitutionen: Sind \sigma_1 und \sigma_2 verallgemeinerte Substitutionen, so definieren wir eine neue verallgemeinerte Substitution \sigma_1 \sigma_2 durch (\sigma_1 \sigma_2)(x) = (x\sigma_1)\sigma_2.

Beispiel: Sei x Variable und t Term. Dann ist \sigma mit $\sigma(y) =\begin{cases} t \quad\text{ falls } x=y \ y \quad\text{ sonst }\end{cases}$ eine verallgemeinerte Substitution. Für alle Terme s und alle atomaren Formeln \alpha gilt s\sigma=s[x:=t] und \alpha\sigma=\alpha[x:=t]. Substitutionen sind also ein Spezialfall der verallgemeinerten Substitutionen.

Beispiel: Die verallgemeinerte Substitution \sigma mit Def(\sigma)=\{x,y,z\} und \sigma(x) =f(h(x′)), \sigma(y) =g(a,h(x′)), \sigma(z) =h(x′) ist gleich der verallgemeinerten Substitution [x:=f(h(x′))] [y:=g(a,h(x′))] [z:=h(x′)] = [x:=f(z)] [y:=g(a,z)] [z:=h(x′)]. Es kann sogar jede verallgemeinerte Substitution \sigma als Verknüpfung von Substitutionen der Form [x:=t] geschrieben werden. Vereinbarung: Wir sprechen ab jetzt nur von „Substitutionen“, auch wenn wir „verallgemeinerte Substitutionen“ meinen.

Lemma

Seien \sigma Substitution, x Variable und t Term, so dass

• (i) x\not\in Def(\sigma) und
• (ii) x in keinem der Terme y\sigma mit y\in Def(\sigma) vorkommt. Dann gilt [x:=t]\sigma=\sigma[x:=t\sigma].

Beispiele: Im folgenden sei t=f(y).

• Ist \sigma=[x:=g(z)], so gilt x[x:=t]\sigma=t\sigma=t\not=g(z) =g(z)[x:=t\sigma] =x\sigma[x:=t\sigma].
• Ist \sigma= [y:=g(x)], so gilt y[x:=t]\sigma=y\sigma=g(x) \not=g(f(g(x)))= g(x) [x:=t\sigma] =y\sigma[x:=t\sigma].
• Ist \sigma= [y:=g(z)], so gelten Def([x:=t]\sigma) =\{x,y\}=Def(\sigma[x:=t\sigma]),[x:=t]\sigma(x) =f(g(z)) =\sigma[x:=t\sigma] und [x:=t]\sigma(y) =\sigma(z) =\sigma[x:=t\sigma], also [x:=t]\sigma=\sigma[x:=t\sigma].

Beweis: Wir zeigen y[x:=t]\sigma=y\sigma[x:=t\sigma] für alle Variablen y.

• y=x: Dann gilt y[x:=t]\sigma=t\sigma. Außerdem y\sigma=x wegen y=x\not\in Def(\sigma) und damit y\sigma[x:=t\sigma]=x[x:=t\sigma]=t\sigma.
• y\not =x: Dann gilt y[x:=t]\sigma=y\sigma und ebenso y\sigma[x:=t\sigma]=y\sigma, da x in y\sigma nicht vorkommt.

Unifikator/Allgemeinster Unifikator

Gegeben seien zwei gleichungsfreie Atomformeln \alpha und \beta. Eine Substitution \sigma heißt Unifikator von \alpha und \beta, falls \alpha\sigma=\beta\sigma.

Ein Unifikator \sigma von \alpha und \beta heißt allgemeinster Unifikator von \alpha und \beta, falls für jeden Unifikator \sigma′ von \alpha und \beta eine Substitution \tau mit \sigma′=\sigma \tau existiert.

Aufgabe: Welche der folgenden Paare (\alpha,\beta) sind unifizierbar?

\alpha	\beta	Ja	Nein
P(f(x))	P(g(y))
P(x)	P(f(y))
Q(x,f(y))	Q(f(u),z)
Q(x,f(y))	Q(f(u),f(z))
Q(x,f(x))	Q(f(y),y)
R(x,g(x),g^2 (x))	R(f(z),w,g(w))

Zum allgemeinsten Unifikator

Eine Variablenumbenennung ist eine Substitution \rho, die Def(\rho) injektiv in die Menge der Variablen abbildet.

Lemma

Sind \sigma_1 und \sigma_2 allgemeinste Unifikatoren von \alpha und \beta, so existiert eine Variablenumbenennung \rho mit \sigma_2=\sigma_1 \rho.

Beweis: \sigma_1 und \sigma_2 allgemeinste Unifikatoren \Rightarrow es gibt Substitutionen \tau_1 und \tau_2 mit \sigma_1\tau_1 =\sigma_2 und \sigma_2\tau_2 =\sigma_1. Definiere eine Substitution \rho durch: $\rho(y) =\begin{cases} y\tau_1 \quad\text{ falls es x gibt, so dass y in } x\sigma_1 \text{ vorkommt}\ y \quad\text{ sonst }\end{cases}$ Wegen Def(\rho)\subseteq Def(\tau_1) ist Def(\rho) endlich, also \rho eine Substitution.

• Für alle Variablen x gilt dann x\sigma_1 \rho=x\sigma_1 \tau_1 =x\sigma_2 und daher \sigma_2 =\sigma_1 \rho.
• Wir zeigen, dass \rho(y) Variable und \rho auf Def(\rho) injektiv ist: Sei y\in Def(\rho). Dann existiert Variable x, so dass y in x\sigma_1 vorkommt. Es gilt x\sigma_1 =x\sigma_2\tau_2=x\sigma_1\tau_1\tau_2, und damit y=y\tau_1 \tau_2 =y\rho \tau_2 =\rho(y)\tau_2, d.h. \rho(y) ist Variable, die Abbildung \rho:Def(\rho)\rightarrow\{z|z\ Variable\} ist invertierbar (durch \tau_2) und damit injektiv.

Unifikationsalgorithmus

• Eingabe: Paar$(\alpha,\beta)$ gleichungsfreier Atomformeln \sigma:= Substitution mit Def(\sigma)=\varnothing (d.h. Identität)
• while \alpha\sigma\not =\beta\sigma do
  • Suche die erste Position, an der sich \alpha\sigma und \beta\sigma unterscheiden
  • if keines der beiden Symbole an dieser Position ist eine Variable
  • then stoppe mit „nicht unifizierbar“
  • else sei x die Variable und t der Term in der anderen Atomformel (möglicherweise auch eine Variable)
    • if x kommt in t vor
    • then stoppe mit „nicht unifizierbar“
    • else \sigma:=\sigma[x:=t]
• endwhile
• Ausgabe: \sigma

Satz

• (A) Der Unifikationsalgorithmus terminiert für jede Eingabe.
• (B) Wenn die Eingabe nicht unifizierbar ist, so terminiert der Unifikationsalgorithmus mit der Ausgabe „nicht unifizierbar“.
• (C) Wenn die Eingabe (\alpha,\beta) unifizierbar ist, dann findet der Unifikationsalgorithmus einen allgemeinsten Unifikator von \alpha und \beta.

(C) besagt insbesondere, daß zwei unifizierbare gleichungsfreie Atomformeln (wenigstens) einen allgemeinsten Unifikator haben. Nach dem Lemma oben haben sie also genau einen allgemeinsten Unifikator (bis auf Umbenennung der Variablen).

Die drei Teilaussagen werden in getrennten Lemmata bewiesen werden.

Lemma (A) Der Unifikationsalgorithmus terminiert für jede Eingabe(\alpha, \beta).

Beweis: Wir zeigen, daß die Anzahl der in \alpha\sigma oder \beta\sigma vorkommenden Variablen in jedem Durchlauf der while-Schleife kleiner wird. Betrachte hierzu einen Durchlauf durch die while-Schleife. Falls der Algorithmus in diesem Durchlauf nicht terminiert, so wird \sigma auf \sigma[x:=t] gesetzt. Hierbei kommt x in \alpha\sigma oder in \beta\sigma vor und der Term t enthält x nicht. Also kommt x weder in \alpha\sigma[x:=t] noch in \beta\sigma[x:=t] vor.

Lemma (B) Wenn die Eingabe nicht unifizierbar ist, so terminiert der Unifikationsalgorithmus mit der Ausgabe „nicht unifizierbar“.

Beweis: Sei die Eingabe (\alpha,\beta) nicht unifizierbar. Falls die Bedingung \alpha\sigma\not=\beta\sigma der while-Schleife irgendwann verletzt wäre, so wäre (\alpha,\beta) doch unifizierbar (denn \sigma wäre ja ein Unifikator). Da nach Lemma (A) der Algorithmus bei Eingabe (\alpha,\beta) terminiert, muss schließlich „nicht unifizierbar“ ausgegeben werden.

Lemma (C1) Sei \sigma′ ein Unifikator der Eingabe (\alpha,\beta), so dass keine Variable aus \alpha oder \beta auch in einem Term aus \{y\sigma′|y\in Def(\sigma′)\} vorkommt. Dann terminiert der Unifikationsalgorithmus erfolgreich und gibt einen Unifikator \sigma von \alpha und \beta aus. Außerdem gibt es eine Substitution \tau mit \sigma′=\sigma\tau.

Beweis:

• Sei N\in\mathbb{N} die Anzahl der Durchläufe der while-Schleife (ein solches N existiert, da der Algorithmus nach Lemma (A) terminiert).
• Sei \sigma_0 Substitution mit Def(\sigma_0) =\varnothing, d.h. die Identität. Für 1\leq i\leq N sei \sigma_i die nach dem $i$-ten Durchlauf der while-Schleife berechnete Substitution \sigma.
• Für 1\leq i\leq N sei x_i die im $i$-ten Durchlauf behandelte Variable x und t_i der entsprechende Term t.
• Für 0\leq i\leq N sei \tau_i die Substitution mit \tau_i(x)=\sigma′(x) für alle x\in Def(\tau_i) =Def(\sigma′)\backslash\{x_1,x_2,...,x_i\}.

Behauptung:

1. Für alle 0\leq i\leq N gilt \sigma′=\sigma_i\tau_i.
2. Im $i$-ten Durchlauf durch die while-Schleife (1\leq i\leq N) terminiert der Algorithmus entweder erfolgreich (und gibt die Substitution \sigma_N aus) oder der Algorithmus betritt die beiden else-Zweige.
3. Für alle 0\leq i\leq N enthalten \{\alpha\sigmai,\beta\sigma_i\} und T_i=\{y\tau_i|y\in Def(\tau_i)\} keine gemeinsamen Variablen.

Aus dieser Behauptung folgt tatsächlich die Aussage des Lemmas:

• Nach (2) terminiert der Algorithmus erfolgreich mit der Substitution \sigma_N. Daher gilt aber \alpha\sigma_N=\beta\sigma_N, d.h. \sigma_N ist ein Unifikator.
• Nach (1) gibt es auch eine Substitution \tau_n mit \sigma′=\sigma_N\tau_n.

Lemma (C) Sei die Eingabe (\alpha,\beta) unifizierbar. Dann terminiert der Unifikationsalgorithmus erfolgreich und gibt einen allgemeinsten Unifikator \sigma von \alpha und \beta aus.

Beweis: Sei \sigma′ ein beliebiger Unifikator von \alpha und \beta. Sei Y=\{y_1,y_2,... ,y_n\} die Menge aller Variablen, die in \{y\sigma′|y\in Def(\sigma′)\} vorkommen. Sei Z=\{z_1,z_2,...,z_n\} eine Menge von Variablen, die weder in \alpha noch in \beta vorkommen. Sei \rho die Variablenumbenennung mit Def(\rho)=Y\cup Z,\rho(y_i) =z_i und \rho(z_i)=y_i für alle 1\leq i\leq n. Dann ist auch \sigma′\rho ein Unifikator von \alpha und \beta und keine Variable aus \alpha oder \beta kommt in einem der Terme aus \{y\sigma′\rho|y\in Def(\sigma′)\} vor. Nach Lemma (C1) terminiert der Unifikationsalgorithmus erfolgreich mit einem Unifikator \sigma von \alpha und \beta, so dass es eine Substitution \tau gibt mit \sigma′\rho=\sigma\tau. Also gilt \sigma′=\sigma(\tau\rho^{-1}). Da \sigma′ ein beliebiger Unifikator von \alpha und \beta war und da die Ausgabe \sigma des Algorithmus nicht von \sigma′ abhängt, ist \sigma also ein allgemeinster Unifikator.

Satz

• (A) Der Unifikationsalgorithmus terminiert für jede Eingabe.
• (B) Wenn die Eingabe nicht unifizierbar ist, so terminiert der Unifikationsalgorithmus mit der Ausgabe „nicht unifizierbar“.
• (C) Wenn die Eingabe (\alpha,\beta) unifizierbar ist, dann findet der Unifikationsalgorithmus immer einen allgemeinsten Unifikator von \alpha und \beta.

(C) besagt insbesondere, daß zwei unifizierbare gleichungsfreie Atomformeln(wenigstens) einen allgemeinsten Unifikator haben. Damit haben sie aber genau einen allgemeinsten Unifikator (bis auf Umbenennung der Variablen).

Prädikatenlogische SLD-Resolution

Erinnerung

• Eine Horn-Klausel der Prädikatenlogik ist eine Aussage der Form \forall x_1 \forall x_2... \forall x_n ((\lnot\bot \wedge\alpha_1 \wedge\alpha_2 \wedge...\wedge\alpha_m)\rightarrow\beta)=\Psi mit m\geq 0, atomaren Formeln \alpha_1,...,\alpha_m und \beta atomare Formel oder \bot. Sie ist definit, wenn \beta\not =\bot.
• E(\varphi) =\{\Psi[x_1 :=t_1 ][x_2 :=t_2 ]...[x_n:=tn]|t_1 ,t_2 ,...,t_n\in D(\sigma)\}
• Eine Horn-Klausel der Aussagenlogik ist eine Formel der Form (\lnot\bot\wedge q_1 \wedge q_2 \wedge... \wedge q_m)\rightarrow r mit m\geq 0, atomaren Formeln q_1,q_2,...,q_m,r atomare Formel oder \bot.

Schreib- und Sprechweise: Für die Horn-Klausel der Prädikatenlogik \forall x_1...\forall x_n(\lnot\bot \wedge \alpha_1 \wedge \alpha_2 \wedge...\wedge \alpha_m)\rightarrow\beta schreiben wir kürzer \{\alpha_1,\alpha_2,...,\alpha_m\}\rightarrow\beta. insbes. \varnothing\rightarrow\beta für \forall x_1...\forall x_n(\lnot\bot\rightarrow\beta)

Erinnerung: Sei \Gamma eine Menge von Horn-Klauseln der Aussagenlogik. Eine aussagenlogische SLD-Resolution aus \Gamma ist eine Folge (M_0 \rightarrow\bot,M_1 \rightarrow\bot,...,M_m\rightarrow\bot) von Hornklauseln mit

• (M_0\rightarrow\bot)\in\Gamma und
• für alle 0\leq n<m existiert (N\rightarrow q)\in\Gamma mit q\in M_n und M_{n+1} =M_n\backslash\{q\}\cup N

Definition

Sei \Gamma eine Menge von gleichungsfreien Horn-Klauseln der Prädikatenlogik. Eine SLD-Resolution aus \Gamma ist eine Folge ((M_0\rightarrow\bot,\sigma_0),(M_1\rightarrow\bot,\sigma_1),...,(M_m\rightarrow\bot,\sigma_m)) von Horn-Klauseln und Substitutionen mit

• (M_0\rightarrow\bot)\in\Gamma und Def(\sigma_0)=\varnothing
• für alle 0\leq n<m existieren \varnothing\not=Q\subseteq M_n,(N\rightarrow\alpha)\in\Gamma und Variablenumbenennung \rho, so dass
  • (N\cup\{\alpha\})\rho und M_n variablendisjunkt sind,
  • \sigma_{n+1} ein allgemeinster Unifikator von \alpha\rho und Q ist und
  • M_{n+1} = (M_n\Q\cup N\rho)\sigma_{n+1}.

Ziel: Seien \Gamma=\{\varphi_1,...,\varphi_n\} Menge gleichungsfreier Horn-Klauseln, \Psi(x_1,x_2 ,...,x_{\iota}) =R(t_1 ,...,t_k) atomare Formel, keine Gleichung und (s_1,...,s_{\iota}) Tupel variablenloser Terme. Dann sind äquivalent:

1. $\Gamma\Vdash\Psi(s_1,...,s_{\iota}).
2. Es gibt eine SLD-Resolution ((M_n\rightarrow\bot,\sigma_n))_{0\leq n\leq m} aus \Gamma\cup\{M_0\rightarrow\bot\} mit M_0=\{\Psi(x_1,...,x_{\iota})\} und M_m=\varnothing und eine Substitution \tau, so dass s_i=x_i\sigma_0 \sigma_1 ...\sigma_m\tau für alle 1\leq i\leq \iota gilt.

Lemma

Sei \Gamma Menge von gleichungsfreien Horn-Klauseln der Prädikatenlogik und (M_n \rightarrow\bot,\sigma_n))_{0\leq n\leq m} eine SLD-Resolution aus \Gamma\cup\{M_0\rightarrow\bot\} mit M_m=\varnothing. Dann gilt \Gamma\Vdash\Psi\sigma_0 \sigma_1\sigma_2...\sigma_m für alle \Psi\in M_0.

Konsequenz: \Gamma=\{\varphi_1,...,\varphi_n\},M_0 =\{\Psi(x_1,...,x_{\iota})\},\tau Substitution, so dass s_i=x_i \sigma_0 \sigma_1 \sigma_2 ...\sigma_m \tau variablenlos für alle 1\leq i \leq \iota. Nach dem Lemma gilt also \Gamma \Vdash\Psi(x_1,...,x_{\iota})\sigma_0 ...\sigma_m und damit \Gamma\Vdash\Psi(x_1 ,...,x_{\iota} )\sigma_0 ...\sigma_m\tau=\Psi(s_1,...,s_{\iota} ). Die Implikation (2)\Rightarrow (1) des Ziels folgt also aus diesem Lemma.

Lemma

Sei \Gamma eine Menge von definiten gleichungsfreien Horn-Klauseln der Prädikatenlogik, sei M\rightarrow\bot eine gleichungsfreie Horn-Klausel und sei \nu Substitution, so dass M\nu variablenlos ist und \Gamma\Vdash M\nu gilt. Dann existieren eine prädikatenlogische SLD-Resolution ((M_n \rightarrow\bot,\sigma_n))_{0 \leq n\leq m} und eine Substitution \tau mit M_0=M,M_m=\varnothing und M_0 \sigma_0 \sigma_1... \sigma_m \tau=M_{\nu}.

Konsequenz: \Gamma=\{\varphi_1,...,\varphi_n\},M=\{\psi(x_1 ,...,x_{\iota})\},s_1,...,s_\iota} variablenlose Terme, so dass \{\varphi_1 ,...,\varphi_n\}\Vdash\psi(s_1,...,s_{\iota}) =\psi(x_1 ,...,x_{\iota})\nu mit \nu(x_i)=s_i. Dann existieren SLD-Resolution und Substitution \tau mit M_0\sigma 0...\sigma_m\tau=M\nu=\{\psi (s_1,...,s_{\iota} )\}. Die Implikation (1)\Rightarrow (2) des Ziels folgt also aus diesem Lemma.

Satz

Sei \Gamma eine Menge von definiten gleichungsfreien Horn-Klauseln der Prädikatenlogik, sei M\rightarrow\bot eine gleichungsfreie Horn-Klausel und sei \nu Substitution, so dass M\nu variablenlos ist. Dann sind äquivalent:

• \Gamma\Vdash M\nu
• Es existieren eine SLD-Resolution ((M_n\rightarrow\bot,\sigma_n))_{0\leq n\leq m} aus \Gamma\cup\{M\nu\rightarrow\bot\} und eine Substitution \tau mit M_0=M,M_m=\varnothing und M_0\sigma_0\sigma_1...\sigma_m\tau=M\nu.

Konsequenz: \Gamma =\{\varphi_1,...,\varphi_n\},M_0 =\{\psi(x_1,...,x_{\iota})\}=\{R(t_1,t_2,...,t_k)\}. Durch SLD-Resolutionen können genau die Tupel variablenloser Terme gewonnen werden, für die gilt: \{\varphi_1,...,\varphi_n\}\Vdash\psi (s_1,...,s_{\iota})

Zusammenfassung Prädikatenlogik

• Das natürliche Schließen formalisiert die „üblichen“ Argumente in mathematischen Beweisen.
• Das natürliche Schließen ist vollständig und korrekt.
• Die Menge der allgemeingültigen Formeln ist semi-entscheidbar, aber nicht entscheidbar.
• Die Menge der Aussagen, die in (\mathbb{N},+,*,0,1) gelten, ist nicht semi-entscheidbar.
• Die SLD-Resolution ist ein praktikables Verfahren, um die Menge der "Lösungen" (s_1,...,s_{\iota}) von \Gamma\Vdash\psi(s_1,...,s_{\iota}) zu bestimmen (wobei \Gamma Menge von gleichungsfreien Horn-Klauseln und \psi Konjunktion von gleichungsfreien Atomformeln sind.

Logische Programmierung

Einführung in die Künstliche Intelligenz (KI)

Ziel: Mechanisierung von Denkprozessen

Grundidee (nach G.W. Leibniz)

1. lingua characteristica - Wissensdarstellungssprache
2. calculus ratiocinator - Wissensverarbeitungskalkül

Teilgebiete der KI

• Wissensrepräsentation
• maschinelles Beweisen (Deduktion)
• KI-Sprachen: Prolog, Lisp
• Wissensbasierte Systeme
• Lernen (Induktion)
• Wissensverarbeitungstechnologien (Suchtechniken, fallbasiertes Schließen, Multiagenten-Systeme)
• Sprach- und Bildverarbeitung

Logische Grundlagen

PROLOG – ein „Folgerungstool“

Sei M eine Menge von Aussagen, H eine Hypothese.

H folgt aus M(M \Vdash H), falls jede Interpretation, die zugleich alle Elemente aus M wahr macht (jedes Modell von M), auch H wahr macht. Für endliche Aussagenmengen M=\{A_1, A_2, ... , A_n\} bedeutet das: M \Vdash H, gdw. ag(\bigwedge_{i=1}^n A_i\rightarrow A) bzw. (was dasselbe ist) kt(\bigwedge_{i=1}^n A_i \wedge \lnot A)

Aussagen in PROLOG: HORN-Klauseln des PK1

A(X_1,...,X_n), A_i(X_1,...,X_n) quantorfreie Atomformeln, welche die allquantifizierten Variablen X_1,...,X_n enthalten können

Varianten / Spezialfälle

1. Regeln (vollständige HORN-Klauseln) \forall X_1... \forall X_n(A(X_1,...,X_n)\leftarrow \bigwedge_{i=1}^n A_i(X_1,...,X_n))
2. Fakten (HORN-Klauseln mit leerem Klauselkörper) \forall X_1...\forall X_n(A(X_1,...,X_n)\leftarrow true)
3. Fragen (HORN-Klauseln mit leerem Klauselkopf) \forall X_1...\forall X_n(false \leftarrow \bigwedge_{i=1}^n A_i(X_1,...,X_n))
4. leere HORN-Klauseln (mit leeren Kopf & leerem Körper) false\leftarrow true

Effekte der Beschränkung auf HORN-Logik

1. Über HORN-Klauseln gibt es ein korrektes und vollständiges Ableitungsverfahren.
   • \{K_1, ...,K_n\} \Vdash H , gdw. \{K_1,...,K_n\} \vdash_{ROB} H
2. Die Suche nach einer Folge von Resolutionsschritten ist algorithmisierbar.
   • Das Verfahren „Tiefensuche mit Backtrack“ sucht systematisch eine Folge, die zur leeren Klausel führt.
   • Rekursive und/oder metalogische Prädikate stellen dabei die Vollständigkeit in Frage.
3. Eine Menge von HORN-Klauseln mit nichtleeren Klauselköpfen ist stets erfüllbar; es lassen sich keine Widersprüche formulieren.
   • K_1 \wedge K_2...\wedge K_n \not= false

Die systematische Erzeugung von (HORN-) Klauseln

1. Verneinungstechnischen Normalform (VTNF): \lnot steht nur vor Atomformeln
   • \lnot\lnot A\equiv A
2. Erzeugung der Pränexen Normalform (PNF): \forall, \exists stehen vor dem Gesamtausdruck
   • \forall X A(X) \rightarrow B \equiv \exists X(A(X)\rightarrow B)
   • \exists X A(X) \rightarrow B \equiv \forall X(A(X)\rightarrow B)
3. Erzeugung der SKOLEM‘schen Normalform (SNF): \exists wird eliminiert Notation aller existenzquantifizierten Variablen als Funktion derjenigen allquantifizierten Variablen, in deren Wirkungsbereich ihr Quantor steht. Dies ist keine äquivalente - , wohl aber eine die Kontradiktorizität erhaltende Umformung.
4. Erzeugung der Konjunktiven Normalform (KNF) Durch systematische Anwendung des Distributivgesetzes A\vee (B\wedge C)\equiv (A\vee B)\wedge(A\vee C) lässt sich aus der SNF \forall X_1...\forall X_n A(X_1,...,X_n) stets die äquivalente KNF \forall X_1...\forall X_n((L_1^1\vee...\vee L_1^{n_1})\wedge...\wedge(L_m^1\vee...\vee L_m^{n_m})) erzeugen. Die L_i^k sind unnegierte oder negierte Atomformeln und heißen positive bzw. negative Literale.
5. Erzeugung der Klauselform (KF) Jede der Elementardisjunktionen (L_1^j \vee...\vee L_1^{j_k}) der KNF kann man als äquivalente Implikation (Klausel) (L_i^j \vee...\vee L_i^{j_m})\leftarrow(L_1^{j_{m+1}}\wedge ...\wedge L_1^{j_k}) notieren, indem man alle positiven Literale L_i^j,...,L_i^{j_m} disjunktiv verknüpft in den DANN-Teil (Klauselkopf) und alle negativen Literale L_i^{j_{m+1}},...,L_i^{j_k} konjunktiv verknüpft in den WENN-Teil (Klauselkörper) notiert.
6. Sind die Klauseln aus Schritt 5. HORN? In dem Spezialfall, dass alle Klauselköpfe dabei aus genau einem Literal bestehen, war die systematische Erzeugung von HORN-Klauseln erfolgreich; anderenfalls gelingt sie auch nicht durch andere Verfahren. Heißt das etwa, die HORN-Logik ist eine echte Beschränkung der Ausdrucksfähigkeit? Richtig, das heißt es.

Im Logik-Teil dieser Vorlesung lernten Sie eine Resolutionsmethode für Klauseln kennenlernen

• ... deren Algorithmisierbarkeit allerdings an der „kombinatorischen Explosion“ der Resolutionsmöglichkeiten scheitert, aber ...
• ... in der LV „Inferenzmethoden“ können Sie noch ein paar „Tricks“ kennenlernen, die „Explosion“ einzudämmen

Inferenz in PROLOG: Resolution nach ROBINSON

gegeben:

• Menge von Regeln und Fakten M M=\{K_1,...,K_n\}
• negierte Hypothese \lnot H \lnot H\equiv \bigwedge_{i=1}^m H_i \equiv false \rightarrow \bigwedge_{i=1}^m H_i

Ziel: Beweis, dass M \Vdash H. kt(\bigwedge_{i=1}^n K_i \wedge \lnot H)

Eine der Klauseln habe die Form A\leftarrow \bigwedge_{k=1}^p B_k. ($A,B_k$- Atomformeln)

Es gebe eine Substitution (Variablenersetzung) \nu für die A und eines der H_i (etwa H_l) vorkommenden Variablen, welche A und H_l syntaktisch identisch macht.

M\equiv \bigwedge_{i=1}^n K_i\wedge \lnot(\bigwedge_{i=1}^m H_i) ist kontradiktorisch (kt\ M‘), gdw. M‘ nach Ersetzen von H durch \bigwedge_{i=1}^{l-1}\nu(H_i)\wedge\bigwedge_{k=1}^p\nu(B_k)\wedge\bigwedge_{i=l+1}^m \nu(H_i) noch immer kontradiktorisch ist.

Jetzt wissen wir also, wie man die zu zeigende Kontradiktorizität auf eine andere – viel kompliziertere Kontradiktorizität zurückführen kann. Für p=0 und m=1 wird es allerdings trivial. Die sukzessive Anwendung von Resolutionen muss diesen Trivialfall systematisch herbeiführen:

Satz von ROBINSON

M'\equiv\bigwedge_{i=1}^n K_i\wedge \lnot H ist kontradiktorisch (kt\ M‘), gdw. durch wiederholte Resolutionen in endlich vielen Schritten die negierte Hypothese \lnot H\equiv false \leftarrow H durch die leere Klausel false\leftarrow true ersetzt werden kann.

Substitution

• Eine (Variablen-) Substitution \nu einer Atomformel A ist eine Abbildung der Menge der in A vorkommenden Variablen X in die Menge der Terme (aller Art: Konstanten, Variablen, strukturierte Terme).
• Sie kann als Menge von Paaren [Variable,Ersetzung] notiert werden: \nu=\{[x,t]: x\in X, t=\nu(x)\}
• Für strukturierte Terme wird die Substitution auf deren Komponenten angewandt: \nu(f(t_1,...,t_n)) = f(\nu(t_1),...,\nu(t_n))
• Verkettungsoperator \circ für Substitutionen drückt Hintereinander-anwendung aus: \sigma\circ\nu(t)=\sigma(\nu(t))
• Substitutionen, die zwei Terme syntaktisch identisch machen, heißen Unifikator: $\nu$unifiziert zwei Atomformeln (oder Terme) s und t (oder: heißt Unifikator von s und t), falls dessen Einsetzung s und t syntaktisch identisch macht.

Unifikation

Zwei Atomformeln p(t_{11},...,t_{1n}) und p_2(t_{21},...,t_{2n}) sind unifizierbar, gdw.

• sie die gleichen Prädikatensymbole aufweisen (p_1= p_2),
• sie die gleichen Stelligkeiten aufweisen (n = m) und
• die Terme t_{1i} und t_{2i} jeweils miteinander unifizierbar sind.

Die Unifizierbarkeit zweier Terme richtet sich nach deren Sorte:

1. Zwei Konstanten t_1 und t_2 sind unifizierbar, gdw. t_1= t_2
2. Zwei strukturierte Terme f(t_{11},...,t_{1n}) und f(t_{21},...,t_{2n}) sind unifizierbar, gdw.
   • sie die gleichen Funktionssymbole aufweisen (f_1= f_2),
   • sie die gleichen Stelligkeiten aufweisen (n=m) und
   • die Terme t_{1i} und t_{2i} jeweils miteinander unifizierbar sind.
3. Eine Variable t_1 ist mit einer Konstanten oder einem strukturierten Term t_2 unifizierbar. t_1 wird durch t_2 ersetzt (instanziert): t_1:= t_2
4. Zwei Variablen t_1 und _2 sind unifizierbar und werden gleichgesetzt: t_1:=t_2 bzw. t_2:= t_1

Genügt „irgendein“ Unifikator?

• ein Beispiel
  • K_1: p(A,B)\leftarrow q(A)\wedge r(B)
  • K_2:q(c)\leftarrow true
  • K_3:r(d)\leftarrow true
  • \lnot H: false\leftarrow p(X,Y)
• Unifikatoren für H_1^0 und Kopf von K_1:
  • \nu^1 = \{[X,a],[Y,b],[A,a],[B,b]\}
  • \nu^2 =\{[X,a],[Y,B],[A,a]\}
  • \nu^3 =\{[X,A],[Y,b],[B,b]\}
  • \nu^4=\{[A,X],[B,Y]\} ...
• Obwohl \{K_1, K_2, K_3\}\Vdash H, gibt es bei Einsetzung von \nu^1, \nu^2 und \nu^3 keine Folge von Resolutionsschritten, die zur leeren Klausel führt.
• Bei Einsetzung von \nu^4 hingegen gibt es eine solche Folge.
• Die Vollständigkeit des Inferenzverfahrens hängt von der Wahl des „richtigen“ Unifikators ab.
• Dieser Unifikator muss möglichst viele Variablen variabel belassen. Unnötige Spezialisierungen versperren zukünftige Inferenzschritte.
• Ein solcher Unifikator heißt allgemeinster Unifikator bzw. "most general unifier" (m.g.u.).

Allgemeinster Unifikator

Eine Substitution heißt allgemeinster Unifikator (most general unfier; m.g.u.) zweier (Atomformeln oder) Terme s und t (\nu= m.g.u.(s,t)), gdw.

1. die Substitution \nu ein Unifikator von s und t ist und
2. für jeden anderen Unifikator \sigma von s und t eine nichtleere und nicht identische Substitution \tau existiert, so dass \sigma=\tau\circ\nu ist. graphisch betrachtet:

Der Algorithmus zur Berechnung des m.g.u. zweier Terme s und t verwendet Unterscheidungsterme: Man lese s und t zeichenweise simultan von links nach rechts. Am ersten Zeichen, bei welchem sich s und t unterscheiden, beginnen die Unterscheidungsterme s* und t* und umfassen die dort beginnenden (vollständigen) Teilterme.

Algorithmus zur Bestimmung des allgemeinsten Unifikators 2er Terme

• input: s, t
• output: Unifizierbarkeitsaussage, ggf. \nu= m.g.u.( s , t )
• i:=0;\nu_i:=\varnothing;s_i:=s; t_i=t
• Start: s_i und t_i identisch?
  • ja \Rightarrow s und t sind unifizierbar, \nu=\nu_i=m.g.u.(s,t) (fertig)
  • nein \Rightarrow Bilde die Unterscheidungsterme s_i^* und t_i^*
    • s_i^* oder t_i^* Variable?
      • nein \Rightarrow s und t sind nicht unifizierbar (fertig)
      • ja \Rightarrow sei (o.B.d.A.) s_i^* eine Variable
        • s_i^* \subseteq t_i^*? (enthält t_i^* die Variable s_i^*?)
          • ja \Rightarrow s und t sind nicht unifizierbar (fertig)
          • nein \Rightarrow
            • \nu':=\{[s,t']: [s,t]\in\nu, t':=t|_{s*\rightarrow t*}\}\cup \{[s_i^*, t_i^*]\}
            • s':=\nu'(s_i); t':=\nu'(t_i); i:=i+1;
            • \nu_i:=\nu'; s_i:=s'; t_i:=t';
            • gehe zu Start

Logische Programmierung

Einordnung des logischen Paradigmas

„deskriptives“ Programmierparadigma =

1. Problembeschreibung
   • Die Aussagenmenge M =\{K_1,...,K_n\}, über denen gefolgert wird, wird in Form von Fakten und Regeln im PK1 notiert.
   • Eine mutmaßliche Folgerung (Hypothese) H wird in Form einer Frage als negierte Hypothese hinzugefügt.
2. (+) Programmverarbeitung
   • Auf der Suche eines Beweises für M \Vdash H werden durch mustergesteuerte Prozedur-Aufrufe Resolutions-Schritte zusammengestellt.
   • Dem „Programmierer“ werden (begrenzte) Möglichkeiten gegeben, die systematische Suche zu beeinflussen.

Syntax

Syntax von Klauseln

	Syntax	Beispiel
Fakt	praedikatensymbol(term,...term).	liefert(xy_ag,motor,vw).
Regel	praedikatensymbol(term,...term) :- praedikatensymbol(term,...term) ,... , praedikatensymbol(term,...term).	konkurrenten(Fa1,Fa2) :- liefert(Fa1,Produkt,),liefert(Fa2,Produkt,).
Frage	?- praedikatensymbol(term,...term) , ... ,praedikatensymbol(term,...term).	?- konkurrenten(ibm,X), liefert(ibm,_,X).

Syntax von Termen

		Syntax	Beispiele
Konstante	Name	Zeichenfolge, beginnend mit Kleinbuchstaben, die Buchstaben, Ziffern und _ enthalten kann.	otto_1 , tisch, hund
	beliebige Zeichenfolge in “...“ geschlossen	“Otto“, “r@ho“
	Sonderzeichenfolge	€%&§$€
Zahl	Ziffernfolge, ggf. mit Vorzeichen, Dezimalpunkt und Exponentendarstellung	3, -5, 1001, 3.14E-12
Variable	allg.	Zeichenfolge, mit Großbuchstaben oder _ beginnend	X, Was, _alter
anonym	Unterstrich	_
strukturierter Term	allg.	funktionssymbol( term , ... , term )	nachbar(chef(X))
Liste	leere Liste	[ ]
	$[term	restliste]$	$[mueller
	[term , term , ... , term ]	[ mueller, mayer, schulze ]

BACKUS-NAUR-Form

• PROLOG-Programm ::= Wissensbasis Hypothese
• Wissensbasis ::= Klausel | Klausel Wissensbasis
• Klausel ::= Fakt | Regel
• Fakt ::= Atomformel.
• Atomformel ::= Prädikatensymbol (Termfolge)
• Prädikatensymbol ::= Name
• Name ::= Kleinbuchstabe |Kleinbuchstabe Restname | "Zeichenfolge" | Sonderzeichenfolge
• RestName ::= Kleinbuchstabe | Ziffer | _ | Kleinbuchstabe RestName | Ziffer RestName | _ RestName
• ...

PROLOG aus logischer Sicht

Was muss der Programmierer tun?

• Formulierung einer Menge von Fakten und Regeln (kurz: Klauseln), d.h. einer Wissensbasis M\equiv\{K_1,...,K_n\}
• Formulierung einer negierten Hypothese (Frage, Ziel) \lnot H\equiv\bigwedge_{i=1}^m H_i \equiv false\leftarrow \bigwedge_{i=1}^m H_i

Was darf der Programmierer erwarten?

• Dass das „Deduktionstool“ PROLOG M \Vdash H zu zeigen versucht, d.h. kt(\bigwedge_{i=1}^n K_i\wedge \lnot H) )
• ..., indem systematisch die Resolutionsmethode auf \lnot H und eine der Klauseln aus M angewandt wird, solange bis \lnot H\equiv false\leftarrow true entsteht

Formulierung von Wissensbasen

1. Beispiel 1 (BSP1.PRO)

• Yoshihito und Sadako sind die Eltern von Hirohito.
  • vater_von(yoshihito,hirohito).
  • mutter_von(sadako,hirohito).
• Kuniyoshi und Chikako sind die Eltern von Nagako.
  • vater_von(kunioshi,nagako).
  • mutter_von(chikako,nagako).
• Akihito‘s und Hitachi‘s Eltern sind Hirohito und Nagako.
  • vater_von(hirohito,akihito).
  • vater_von(hirohito,hitachi).
  • mutter_von(nagako,akihito).
  • mutter_von(nagako,hitachi).
• Der Großvater ist der Vater des Vaters oder der Vater der Mutter.
  • grossvater_von(G,E) :- vater_von(G,V), vater_von(V,E).
  • grossvater_von(G,E) :-vater_von(G,M),mutter_von(M,E).
• Geschwister haben den gleichen Vater und die gleiche Mutter.
  • geschwister(X,Y) :- vater_von(V,X), vater_von(V,Y), mutter_von(M,X), mutter_von(M,Y).

Visual Prolog benötigt aber einen Deklarationsteil für Datentypen und Aritäten der Prädikate, der für die o.g. Wissensbasis so aussieht:

domains
  person = symbol
predicates
  vater_von(person,person)        % bei nichtdeterministischen Prädikaten
  mutter_von(person,person).      % kann man „nondeterm“ vor das
  grossvater_von(person,person)   % Prädikat schreiben, um die
  geschwister(person,person)      % Kompilation effizienter zu machen
clauses
  < Wissensbasis einfügen und Klauseln gleichen Kopfprädikates gruppieren>
goal
  < Frage ohne „?-“ einfügen>

2. Beispiel 2 (BSP2.PRO)

• Kollegen Meier und Müller arbeiten im Raum 1, Kollege Otto im Raum 2 und Kollege Kraus im Raum 3.
  • arbeitet_in(meier,raum_1).
  • arbeitet_in(mueller,raum_1).
  • arbeitet_in(otto,raum_2).
  • arbeitet_in(kraus,raum_3).
• Netzanschlüsse gibt es in den Räumen 2 und 3.
  • anschluss_in(raum_2).
  • anschluss_in(raum_3).
• Ein Kollege ist erreichbar, wenn er in einem Raum mit Netzanschluss arbeitet.
  • erreichbar(K) :- arbeitet_in(K,R),anschluss_in(R).
• 2 Kollegen können Daten austauschen, wenn sie im gleichen Raum arbeiten oder beide erreichbar sind.
  • koennen_daten_austauschen(K1,K2) :- arbeitet_in(K1,R),arbeitet_in(K2,R).
  • koennen_daten_austauschen(K1,K2) :- erreichbar(K1),erreichbar(K2).

Deklarationsteil

domains
  person, raum: symbol
predicates
  arbeitet_in(person,raum)
  ansluss_in(raum)
  erreichbar(person)
  koennen_daten_austauschen(person,person)
clauses
  ...
goal
  ...

Verarbeitung Logischer Programme

Veranschaulichung ohne Unifikation

Tiefensuche mit Backtrack: Es werden anwendbare Klauseln für das erste Teilziel gesucht. Gibt es ...

• ... genau eine, so wird das 1. Teilziel durch deren Körper ersetzt.
• ... mehrere, so wird das aktuelle Ziel inklusive alternativ anwendbarer Klauseln im Backtrack-Keller abgelegt und die am weitesten oben stehende Klausel angewandt.
• ... keine (mehr), so wird mit dem auf dem Backtrack-Keller liegendem Ziel die Bearbeitung fortgesetzt.

Dies geschieht solange, bis

• das aktuelle Ziel leer ist oder
• keine Klausel (mehr) anwendbar ist und der Backtrack-Keller leer ist.

Veranschaulichung mit Unifikation

Zusätzliche Markierung der Kanten mit der Variablenersetzung (dem Unifikator).

PROLOG aus prozeduraler Sicht

Beispiel: die „Hackordnung“

1. chef_von(mueller,mayer).
2. chef_von(mayer,otto).
3. chef_von(otto,walter).
4. chef_von(walter,schulze).
5. weisungsrecht(X,Y) :- chef_von(X,Y).
6. weisungsrecht(X,Y) :- chef_von(X,Z), weisungsrecht(Z,Y).

Deklarative Interpretation In einem Objektbereich I=\{mueller, mayer, schulze, ...\} bildet das Prädikat weisungsrecht(X,Y) [X,Y] auf wahr ab, gdw.

• das Prädikat chef_von(X,Y) das Paar [X,Y] auf wahr abbildet oder
• es ein Z\in I gibt, so dass
  • das Prädikat chef_von(X,Z) das Paar [X,Z] auf wahr abbildet und
  • das Prädikat weisungsrecht(Z,Y) das Paar [Z,Y] auf wahr abbildet.

Prozedurale Interpretation Die Prozedur weisungsrecht(X,Y) wird abgearbeitet, indem

1. die Unterprozedur chef_von(X,Y) abgearbeitet wird. Im Erfolgsfall ist die Abarbeitung beendet; anderenfalls werden
2. die Unterprozeduren chef_von(X,Z) und weisungsrecht(Z,Y) abgearbeitet; indem systematisch Prozedurvarianten beider Unterprozeduren aufgerufen werden.Dies geschieht bis zum Erfolgsfall oder erfolgloser erschöpfender Suche.

deklarative Interpretation	prozedurale Interpretation
Prädikat	Prozedur
Ziel	Prozeduraufruf
Teilziel	Unterprozedur
Klauseln mit gleichem Kopfprädikat	Prozedur-varianten
Klauselkopf	Prozedurkopf
Klauselkörper	Prozedurrumpf

Die Gratwanderung zwischen Wünschenswertem und technisch Machbarem erfordert mitunter „Prozedurales Mitdenken“, um

1. eine gewünschte Reihenfolge konstruktiver Lösungen zu erzwingen,
2. nicht terminierende (aber – deklarativ, d.h. logisch interpretiert - völlig korrekte) Programme zu vermeiden,
3. seiteneffektbehaftete Prädikate sinnvoll einzusetzen,
4. (laufzeit-) effizienter zu programmieren und
5. das Suchverfahren gezielt zu manipulieren.

Programm inkl. Deklarationsteil (BSP3.PRO)

domains
  person = symbol
predicates
  chef_von(person,person)
  weisungsrecht(person,person)
clauses
  chef_von(mueller,mayer).
  chef_von(mayer,otto).
  chef_von(otto,walter).
  chef_von(walter,schulze).
  weisungsrecht(X,Y) :- chef_von(X,Y).
  weisungsrecht(X,Y) :- chef_von(X,Z), weisungsrecht(Z,Y).
goal
  weisungsrecht(Wer,Wem).

Prädikate zur Steuerung der Suche nach einer Folge von Resolutionsschritten!

!(cut) Das Prädikat !/0 ist stets wahr. In Klauselkörpern eingefügt verhindert es ein Backtrack der hinter !/0 stehenden Teilziele zu den vor !/0 stehenden Teilzielen sowie zu alternativen Klauseln des gleichen Kopfprädikats. Die Verarbeitung von !/0 schneidet demnach alle vor der Verarbeitung verbliebenen Lösungswege betreffenden Prozedur ab.

Prädikate zur Steuerung der Suche: $!/0$

Prädikate zur Steuerung der Suche nach einer Folge von Resolutionsschritten fail Das Prädikat fail/0 ist stets falsch. In Klauselkörpern eingefügt löst es ein Backtrack aus bzw. führt zum Misserfolg, falls der Backtrack-Keller leer ist, d.h. falls es keine verbleibenden Lösungswege (mehr) gibt.

Listen und rekursive Problemlösungsstrategien

Listen

1. [] ist eine Liste.
2. Wenn T ein Term und L eine Liste ist, dann ist
   1. [T|L] eine Liste.
   2. T.L eine Liste. (ungebräuchlich)
   3. .(T,L) eine Liste. (ungebräuchlich) Das erste Element T heißt Listenkopf, L heißt Listenkörper oder Restliste.
3. Wenn t_1, ... ,t_n Terme sind, so ist [t_1,...,t_n] eine Liste.
4. Weitere Notationsformen von Listen gibt es nicht.

Listen als kompakte Wissensrepräsentation: ein bekanntes Beispiel (BSP5.PRO)

• arbeiten_in([meier, mueller], raum_1).
  • arbeitet_in(meier, raum_1).
  • arbeitet_in(mueller, raum_1).
• arbeitet_in(otto, raum_2).
  • arbeiten_in([otto], raum_2 ).
• arbeitet_in(kraus, raum_3).
  • arbeiten_in([kraus], raum_3 ).
• anschluesse_in([raum_2, raum_3]).
  • anschluss_in(raum_2).
  • anschluss_in(raum_3).

Rekursion in der Logischen Programmierung Eine Prozedur heißt (direkt) rekursiv, wenn in mindestens einem der Klauselkörper ihrer Klauseln ein erneuter Aufruf des Kopfprädikates erfolgt. Ist der Selbstaufruf die letzte Atomformel des Klauselkörpers der letzten Klausel dieser Prozedur - bzw. wird er es durch vorheriges „Abschneiden“ nachfolgender Klauseln mit dem Prädikat !/0 - , so spricht man von Rechtsrekursion ; anderenfalls von Linksrekursion. Eine Prozedur heißt indirekt rekursiv, wenn bei der Abarbeitung ihres Aufrufes ein erneuter Aufruf derselben Prozedur erfolgt.

Wissensverarbeitung mit Listen: (BSP5.PRO)

• erreichbar(K) :- arbeitet_in(K,R), anschluss_in(R).
  • erreichbar(K) :- anschluesse_in(Rs), member(R, Rs), arbeiten_in(Ks, R), member(K, Ks).
• koennen_daten_austauschen(K1,K2) :- arbeitet_in(K1,R),arbeitet_in(K2,R).
  • koennen_daten_austauschen(K1,K2) :- arbeiten_in(Ks,_),member(K1,Ks), member(K2,Ks).
• koennen_daten_austauschen(K1,K2) :- erreichbar(K1),erreichbar(K2).
  • koennen_daten_austauschen(K1,K2) :- erreichbar(K1),erreichbar(K2).

BSP5.PRO

domains
  person, raum = symbol
  raeume = raum*
  personen = person*
predicates
  arbeiten_in(personen, raum)
  anschluesse_in(raeume)
  erreichbar(person)
  koennen_daten_austauschen(person,person)
  member(person,personen)
  member(raum,raeume)
clauses
  ... (siehe oben)
  member(E,[E|_]).
  member(E,[_|R]) :- member(E,R).
goal
  erreichbar(Wer).

Unifikation 2er Listen

1. Zwei leere Listen sind (als identische Konstanten aufzufassen und daher) miteinander unifizierbar.
2. Zwei nichtleere Listen [K_1|R_1] und [K_2|R_2] sind miteinander unifizierbar, wenn ihre Köpfe (K_1 und K_2) und ihre Restlisten (R_1 und R_2) jeweils miteinander unifizierbar sind.
3. Eine Liste L und eine Variable X sind miteinander unifizierbar, wenn die Variable selbst nicht in der Liste enthalten ist. Die Variable X wird bei erfolgreicher Unifikation mit der Liste L instanziert: X:=L.